Pendelbewegung in Geogebra
Animationen gehobener Art
Geogebra eignet sich hervorragend, um die Funktion von technischen Konstruktionen zu demonstrieren. Anhand eines Pendels wird demonstriert, dass der Einstieg in die Welt der Animation keine Mühe bereitet.
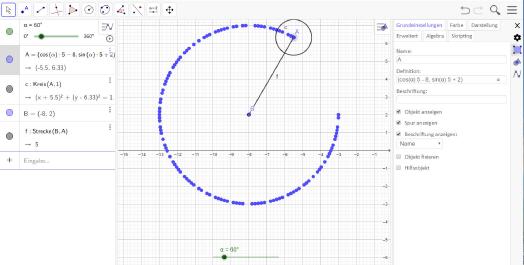
Pendelbewegungen sind in Glocken ebenso zu beobachten, wie in Uhren. Mit Geogebra lässt sich dieser Bewegungsablauf relativ einfach umsetzen. Nötig sind für einen ersten Einstieg lediglich eine Gerade, ein Kreis sowie ein Schieberegler. Der Kreis sollte an Punkt -3,2 platziert werden. Der Startpunkt für die Strecke ist auf Punkt -8,2 zu setzen und der Streckenendpunkt auf Punkt A.
Um in der Animation unnötige Rechenoperationen zu vermeiden, ist darauf zu achten, dass der Kreis über die Funktion ›Kreis mit Mittelpunkt und Radius‹ erzeugt wird.
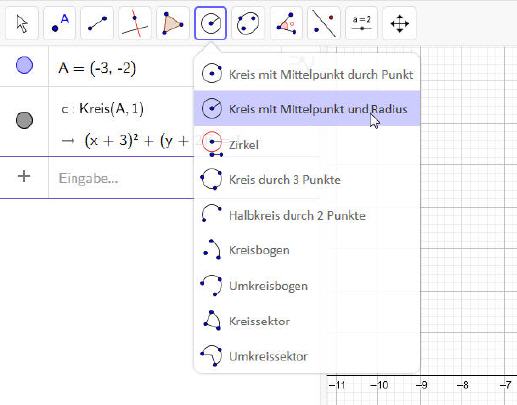
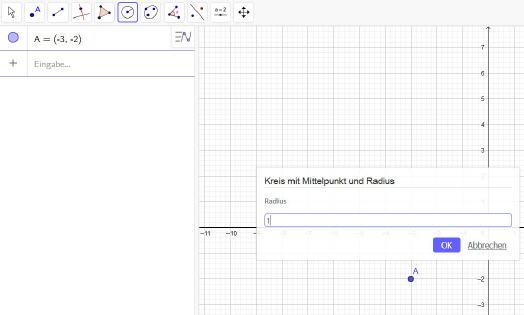
Die Größe des Kreises wird hier über die Eingabe eines Zahlenwertes festgelegt. In diesem Beispiel ist ein Radius von 1 zu wählen.
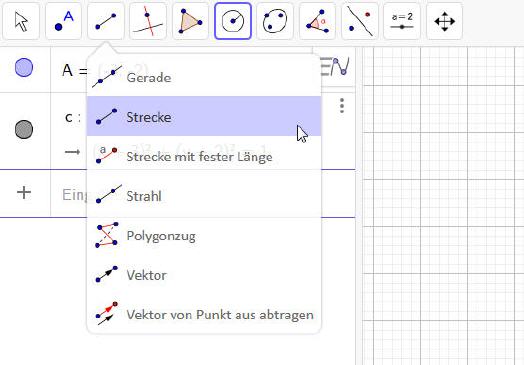
Anschließend wird eine Strecke ausgewählt und eingezeichnet. Wie erwähnt sollte der Startpunkt der Strecke bei -8,2 liegen, der Endpunkt ist hingegen auf Punkt A zu setzen.
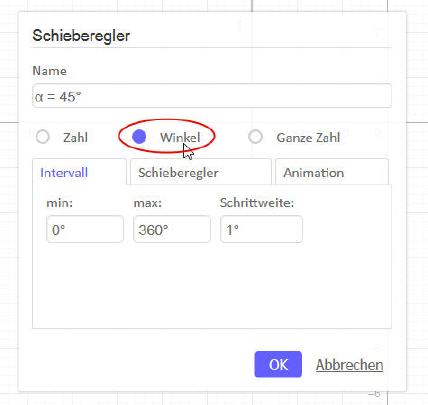
Danach ist ein Schieberegler auf dem Zeichenfeld zu platzieren. Dabei ist allerdings zu beachten, dass dieser Schieberegler in Grad arbeiten muss. Die min.- und max-Werte können zunächst unverändert übernommen werden.
Das Ergebnis sieht wie folgt aus:
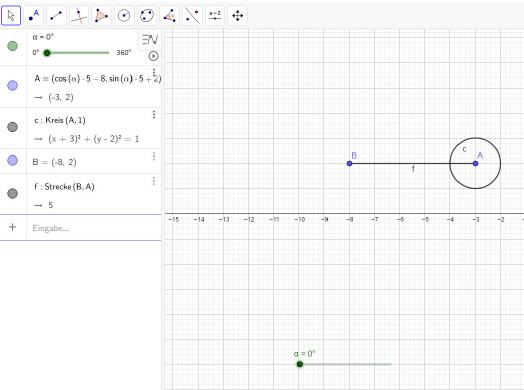
Nun muss dafür gesorgt werden, dass Punkt ›A‹ sich auf einer Kreisbahn bewegt, wenn der Schieberegler bewegt wird. Dazu muss die Definition von Punkt A angepasst werden. Es gilt, hier die passende Formel aus der Trigonometrie auszuwählen, um dies vorzunehmen.
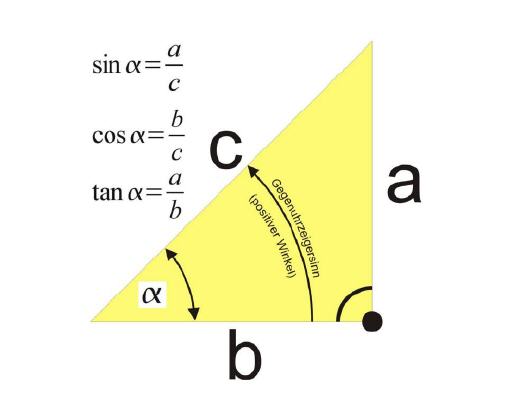
Nähere Infos zu trigonometrischen Berechnungen finden Sie hier:
Die korrekte Formel für die X-Achse lautet:
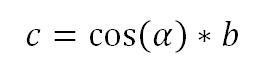
Nun muss noch die eingezeichnete Position des Kreismittelpunkte in der X-Achse berücksichtigt werden:
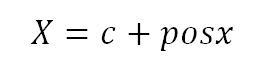
In gleicher Weise muss für die Y-Achse vorgegangen werden:
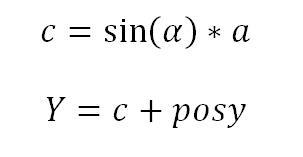
Angenommen, es sind folgende Werte bekannt:
Punkt A (X): -3
Punkt A (Y): 4
Punkt B (X): -8
Punkt B (Y): 2
Radius: 1
Länge von c: 5
Winkel Alpha: 0 Grad
Dann ergeben sich folgende Werte:
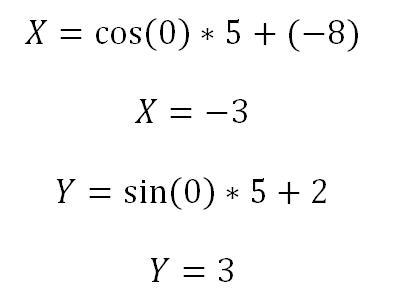
Der Mittelpunkt des Punktes A liegt bei einem Winkel Alpha von Null Grad unverändert an seinem Ursprünglichen Punkt, nämlich bei X-3 und Y3. Wenn der Winkel beispielsweise auf 20 Grad verändert wird, so verändert sich die Lage von Punkt A wie folgt:
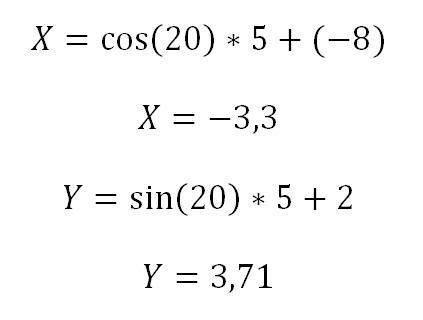
Die ermittelten Formeln sind wie folgt einzugeben:
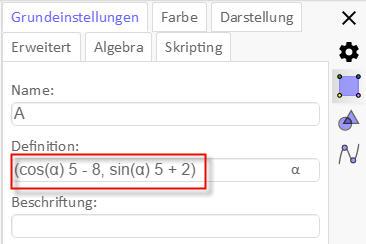
Danach kann der Schieber für den Winkeldurchlauf bewegt werden. Es zeigt sich, dass sich Punkt A auf einer Kreisbahn um Punkt B bewegt. Eine Animation dieser Bewegung kann durch Aktivieren der Schieberfunktion ›Animation ein‹ erreicht werden, die im Reiter ›Grundeinstellungen‹ zu finden ist.
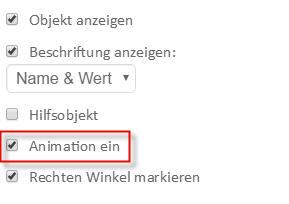
Die Geschwindigkeit, mit der die Animation abläuft, ist durch Klick auf den entsprechenden Bereich im Fenster des entsprechenden Schiebers änderbar.
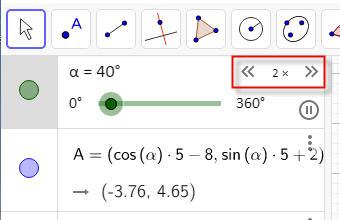
Geogebra bietet natürlich Funktionen, die es erlauben, die Pendelbewegungen zu kontrollieren. Dazu steht das Auswahlfeld ›Wiederholen‹ im Reiter ›Schieberegler‹ zur Verfügung.
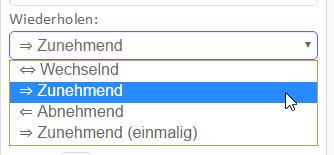
Folgende Funktionen sind möglich:
Wechselnd: Die Animation wird beim Erreichen des Endwinkels in der jeweils anderen Richtung fortgesetzt (Pendelbewegung).
Zunehmend: Die Animation wird endlos im Gegenuhrzeigersinn ausgeführt.
Abnehmend: Die Animation wird endlos im Uhrzeigersinn ausgeführt.
Zunehmend (einmalig): Die Animation wird einmal bis zum Endwinkel ausgeführt, danach gestoppt.
Gelegentlich ist es erwünscht, den Weg einer Animation zu verfolgen. Auch dies ist möglich, da es in Geogebra die Funktion ›Spur anzeigen‹ unter dem Reiter ›Grundeinstellungen‹ gibt.
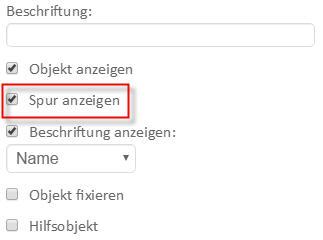
Sobald die Animation gestartet ist, wird deren Spur eingezeichnet.

Soll nun ein Pendel simuliert werden, so muss zunächst festgelegt werden, innerhalb welchen Winkels die Pendelbewegung stattfinden soll. Dies erfolgt im entsprechenden Eingabefeld im Reiter ›Schieberegler‹.
Bei der Eingabe von Beispielsweise 250 und 290 Grad für die Endstellungen ist unbedingt darauf zu achten, dass in der virtuellen Tastatur das Grad-Symbol am Ende der Zahl eingefügt und anschließend die Return-Taste dieser virtuellen Tastatur zur Eingabe-Quittierung genutzt wird, da die Return-Taste der realen Tastatur in diesem Fall zum Verwerfen der getätigten Eingabe führt.
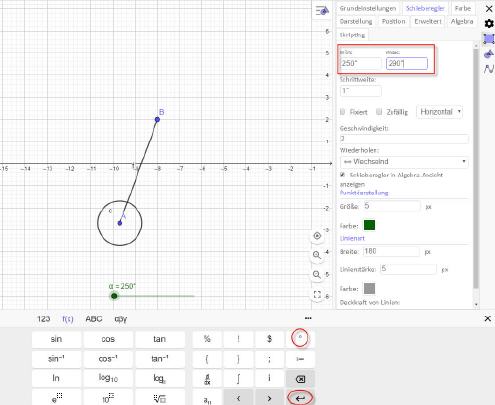
Wird nun wieder ›Wiederholen‹ auf ›Wechselnd‹ gestellt, so kann ein Pendel bewundert werden, dessen Geschwindigkeit sich auf die bereits erwähnte Weise regeln lässt.
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 4 - gesamt: 8220.















































































