Die Arbeitsweise des Excel Solvers verstehen
Ein mächtiges Excel-Tool besser kennenlernen
Der in Excel integrierte Solver ist ein nützliches Stück Software. Damit man mit dem Programm zurechtkommt, ist es allerdings nötig, seine Funktionsweise zu verstehen. Doch egal ob Printmedium oder Onlinequelle – leider ist diesbezüglich oft nur schwer Verständliches zu lesen, weshalb viele Interessenten einen weiten Bogen um diese clevere Software machen. Zeit, ein wenig Licht auf einen interessanten Problemlöser zu lenken.
Egal, ob Projektplanung, Budgetfindung oder Zahnradberechnung – überall dort, wo es gilt, ohne zeitraubende Trial-and-Error-Versuche exakte Werte zu ermitteln, ist der Solver von Excel in seinem Element. In rasantem Tempo probiert diese Software unterschiedliche Zahlen durch, um zielgenau diejenigen Werte zu finden, die der User so dringend sucht, um ein Rechenproblem zu lösen.
Wer den Solver umfassend ausreizen will, tut gut daran, seine Funktionsweise zu ergründen. Doch bevor dies möglich ist, muss dieser zunächst aktiviert werden, da es sich hier um ein Add-In handelt, das nicht von Haus aus in Excel aktiv ist.
Aktivierung des Solvers in Excel 2010
Nachfolgend wird die Aktivierung des Solvers in Excel 2010 beschrieben. Die Grundsätzliche Vorgehensweise unterscheidet sich jedoch in den verschiedenen Excel-Versionen nicht.
Zunächst in der Registerkarte ›Datei‹ auf ›Optionen‹ klicken.
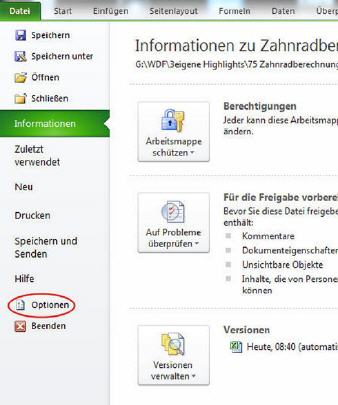
Danach auf ›Add-Ins‹ klicken und im Feld ›Verwalten‹ die Option ›Excel-Add-Ins‹ auswählen.
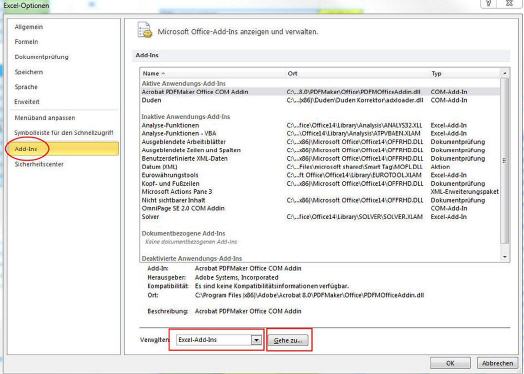
Nun auf ›Gehe zu…‹ klicken und in der erscheinenden Add-In-Liste das Kontrollkästchen ›Solver‹ auswählen. Anschließend auf den Button ›OK‹ klicken.
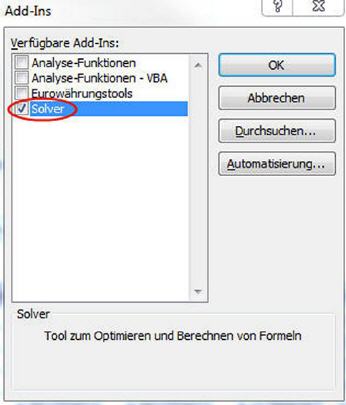
Der Solver ist nun aktiv und kann in der Registerkarte ›Daten‹ ab sofort in der Gruppe ›Analyse‹ aufgerufen werden.
Funktionsweise des Solvers
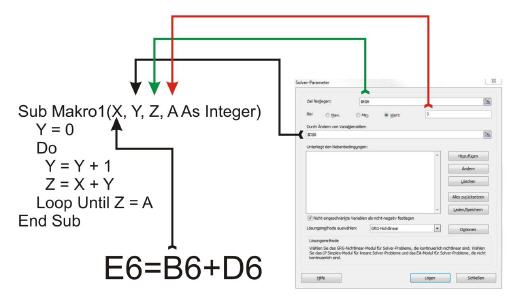
Der Solver ist eigentlich nichts anderes, als die Eingabemaske für eine im Hintergrund laufende Schleife, in der eine Formel mit immer neuen Werten bestückt wird. Diese Schleife wird solange durchlaufen, bis in den Variablen diejenigen Werte stehen, mit denen der vorgegebene Ausgangswert erreicht wird.
Raffiniert ist nun, dass die Formel aus der Excel-Tabelle übernommen wird und die dort aufgeführten Variablen mit jedem Durchlauf mit neuen Werten bestückt werden. Das Ergebnis wird mit dem vorgegeben Ziel verglichen und bei Abweichungen verworfen. Andernfalls wird der Schleifendurchlauf gestoppt und die gefundenen Werte ausgegeben.
Ein einfaches Beispiel:
Es macht viel Sinn, den Solver anhand eines sehr einfachen Beispiels zu erläutern, um dessen Arbeitsweise verstehen zu lernen, was schlussendlich die Anwendung des Solvers an komplizierten Aufgaben erleichtert. Angenommen, es ist folgende Aufgabe bekannt: 1+2=3. Natürlich braucht es nun keinen Solver, um herauszufinden, welche Zahl gesucht ist, wenn nur ein Wert und das Ergebnis bekannt sind: 1+?=3. Dennoch soll dieses Beispiel einmal in einer Excel-Tabelle eingegeben werden, da es hier darum geht, die Arbeitsweise eines Solvers verstehen zu lernen.
Wird ein entsprechendes Excel-Blatt erstellt und das Feld für Wert 2 freigelassen, so berechnet Excel als Ergebnis den Wert ›1‹, da 1+0=1 entspricht. In dieser einfachen Aufgabe soll nun der Solver herausfinden, welcher Wert in D6 stehen muss, damit als Ergebnis die Zahl 3 herauskommt.
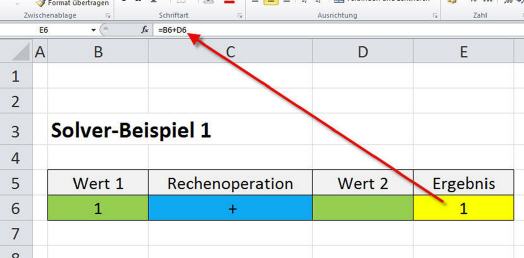
Der Solver bekommt über seine Eingabemaske alle zur Berechnung nötigen Werte. ›Ziel festlegen‹ bedeutet: Zelle ›E6‹ ist diejenige Zelle, in der später der gesuchte Wert einzutragen ist, der in diesem Beispiel ›3‹ betragen muss. In dieser Zelle befindet sich zudem die Formel, mit der gerechnet wird. In diesem Beispiel lautet die Formel: B6+D6. Das Eingabefeld ›Durch Ändern von Variablenzellen‹ bedeutet, dass der Solver in dieser Zelle den gesuchten Wert ermitteln soll, der zum gewünschten Ergebnis führt.
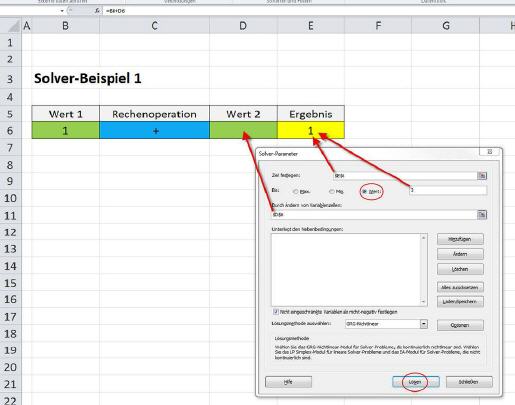
Als Lösungsmethode können für dieses Beispiel ›GRP-Nichtlinear‹ oder ›Simplex LP‹ gewählt werden. Nach Klick auf den Button ›Lösen‹ berechnet der Solver die gesuchte Zahl und gibt eine Meldung aus. Ist die Lösung korrekt, kann diese durch Klick auf den Button ›OK‹ in die Zelle übernommen werden.
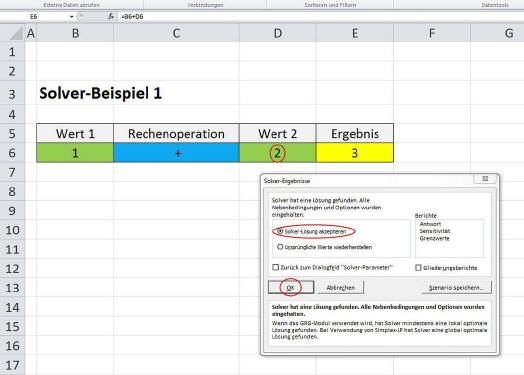
Hinweis: Ergebnisse können nach der Werteübernahme nicht mehr rückgängig gemacht werden. Ein neues Ergebnis mit anderen Ausgangswerten bedarf eines neuen Solverlaufs.
Das passiert im Hintergrund:
Wie angedeutet, ist das Solver-Fenster lediglich eine Eingabemaske, um eine im Hintergrund laufende Berechnungsschleife mit Werten zu versorgen.
Als Rechenformel wird die in Zelle E6 stehende Formel verwendet:
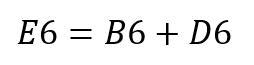
Der Zusammenhang:

Natürlich ist das Programm für den Solver von Microsoft komplizierter aufgebaut. Schließlich müssen weit umfangreichere Rahmenbedingungen vom Solver berücksichtigt werden. Hier geht es jedoch um das Verständnis der grundlegenden Funktion: Die im Hintergrund laufende Schleife wird so lange durchlaufen., bis das Ergebnis der Variablen ›Z‹ dem Vorgabewert in Variable ›A‹ entspricht.
Nicht immer ist es jedoch machbar, dass beide Variablen exakt in Übereinstimmung zu bringen sind. Schon einfaches Wurzelziehen oder trigonometrische Funktionen sorgen dafür, dass die Wahrscheinlichkeit einer Übereinstimmung unwahrscheinlich wird. Fließkommazahlen und Rundungsfehler werden zum Problem.
Doch auch für diese Fälle gibt es Lösungen: Die Angabe von Nebenbedingungen. Sobald der Solver eine Übereinstimmung festgestellt hat, bricht er ab und präsentiert das Ergebnis.
Wurzelziehen mit dem Solver
Folgende Formel soll als Grundlage dienen:
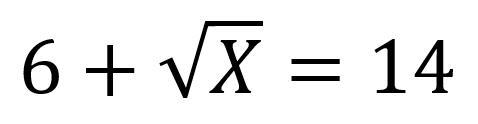
Angenommen, die Zahl, aus der die Wurzel gezogen werden soll, ist unbekannt. Bekannt sind lediglich das Ergebnis und die Zahl 6. Um die gesuchte Zahl zu finden, ist die Tabelle wir folgt aufzubauen: 6=B6; gesuchter Wert=D6; Ergebnis=E6. Die Formel in Zelle E6 lautet: =B6+Wurzel(D6).
Der Solver wird gestartet und mit folgenden Eingaben ergänzt: Ziel festlegen=$E$6; Bis=14; Durch Ändern von Variablenzellen=$D$6.
Nach Klick auf ›Lösen‹ wird erkennbar, dass der Solver kein sauberes Ergebnis abliefert. Er hat für den gesuchten ›Wert 2‹ die Zahl 64,0000908 gefunden, was zum Ergebnis 14,0000057 führt. Diese Abweichung ist unter Umständen unbefriedigend. Doch handelt es sich beim Solver eben um ein Werkzeug, das Gleichungen lediglich näherungsweise lösen kann.
Diese Einschränkungen lassen sich jedoch mit sogenannten Nebenbedingungen ausgleichen, wie nachfolgend gezeigt wird.
Lösung mit zwei Unbekannten
Der Solver ist natürlich in der Lage, auch Formelausdrücke mit mehreren Unbekannten zu berechnen. Dazu soll obige Formel in folgende Formel abgewandelt werden:
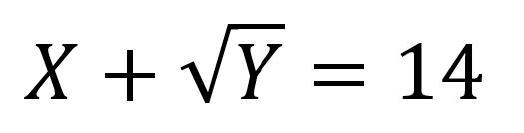
Mit den gleichen Einstellungen wie zuvor gestartet, findet der Solver folgende Zahlen: X (Wert 1)=3,79461309; Y (Wert 2) = 104,149922.
Wie eine Überprüfung mit dem Taschenrechner zeigt, wird der gesuchte Wert 14 exakt getroffen.
Hinzufügen von Nebenbedingungen
Über die Bestimmung von Nebenbedingungen lässt sich der Rechenweg des Solvers gezielt beeinflussen. Ist es zum Beispiel erwünscht, dass die Zelle B6 (Wert 1) auf jeden Fall mit der Zahl 6 vor dem Solverlauf gefüllt wird, so kann man dies in den Nebenbedingungen festlegen. Dazu den Button ›Hinzufügen‹ anklicken und als Zellbezug die Zelle B6 sowie das =-Zeichen wählen und in das Feld ›Nebenbedingung‹ die Zahl 6 eintragen.
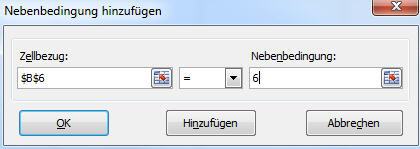
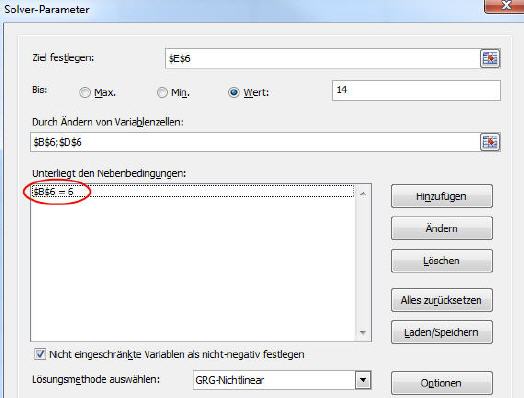
Interessant ist, dass ein nachfolgender Solverlauf ein genaueres Ergebnis bezüglich des gesuchten Wurzelwerts zutage fördert, als wenn der Wert 6 direkt in die Zelle geschrieben worden wäre: 64,0000042. Dies zeigt, dass es manchmal lohnt, ungewöhnliche Wege zu gehen, um noch exaktere Lösungen mit dem Solver zu finden.
Doch ist das Ergebnis immer noch unbefriedigend, da immer noch eine Abweichung zum Wert 64 vorhanden ist, aus dem das exakte Ergebnis von 14 zu bilden wäre. Die Lösung liegt darin, dem Solver zu sagen, dass D6 (Wert 2) ganzzahlig zu sein hat. In der EDV werden solche Zahlen als Integer-Zahlen bezeichnet. Diese können übrigens auch auf guten Taschenrechnern eingestellt werden. Die zuständige Taste besitzt den Aufdruck ›INT‹.
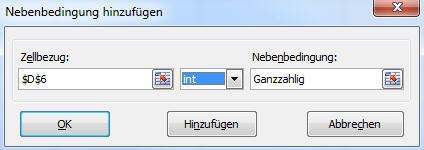
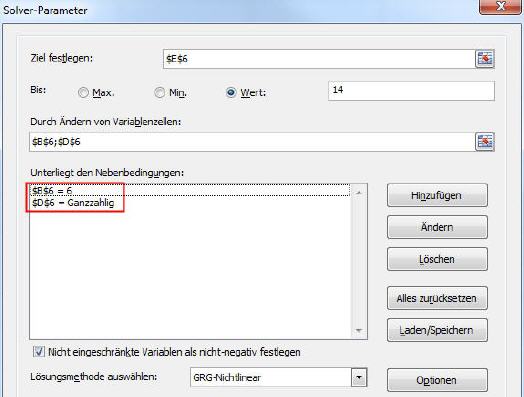
Die Nebenbedingung wird in den Solver auf die gleiche Weise eingetragen, wie schon in der ersten Nebenbedingung geschehen. Wird der Solver nun gestartet, so findet er exakt die gewünschten Zahlen, nämlich 64 für die Wurzelrechnung und 14 als Ergebnis.
Download
Eine Excel-Tabelle mit Solver-Übungen finden Sie hier [18 KB] .
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 1 - gesamt: 22417.















































































