Berührpunktberechnung Tangente an zwei Kreisen
Geometrierechnen leicht gemacht
Wenn es gilt, die Berührpunkte einer Geraden an zwei Kreisen zu ermitteln, bietet sich die Dreiecksberechnung an. Die Dreiecksberechnung ist ein Tausendsassa in der Geometrie. Es gibt nahezu kein Problem, das damit nicht gelöst werden kann. Die Ermittlung der beiden Berührpunkte ist mit deren Hilfe rasch erledigt.
Wie bereits bei den vorhergehenden Kursen angesprochen, gilt auch diesmal folgender Rat: Bevor dieses Manuskript durchgearbeitet wird, empfiehlt sich die Lektüre des Skripts ›Berechnung der Schnittpunkte zwischen zwei Kreisen‹, das hier zu finden ist. Erst mit dieser Grundlage kann an dieser Stelle sinnvoll weitergelesen werden, da sonst wesentliche Dinge unbekannt bleiben.
Folgende Beschreibung erhebt keinen Anspruch, den besten Rechenweg zur Berechnung einer Tangente an zwei Kreisen zu beschreiben. Wie hinreichend bekannt, führen immer mehrere Wege ans Ziel. Nicht alle Wege sind jedoch für jeden gleichermaßen geeignet. Der vorgeschlagene Lösungsweg zum Berechnen einer Tangente, die sich beim Berühren einer Geraden an einem Punkt eines Kreise ergibt, ist daher nicht unbedingt jedermanns Favorit. Er kommt jedoch den Fachleuten entgegen, die gerne die Dreiecksberechnung zur Lösung geometrischer Aufgaben heranziehen.
Wenn eine Gerade einen Kreis berührt, spricht man von einer Tangente. Um die beiden Berührpunkte zu berechnen, die sich ergeben, wenn eine Tangente zwei Kreise tangiert, ist die Dreiecksberechnung eine gute Wahl. Schritt für Schritt nähert man sich hier der Lösung.
Folgende Startpunkte aller Geraden sind bekannt:
| SP1 | X | 101,3202 mm |
| SP1 | Y | -13,7293 mm |
| SP2 | X | 39,2222 mm |
| SP2 | Y | 107,6833 mm |
| SP3 | X | 49,2293 mm |
| SP3 | Y | 119,3583 mm |
| SP4 | X | 178,7109 mm |
| SP4 | Y | 76,5598 mm |
| SP5 | X | 82,9279 mm |
| SP5 | Y | 1,3529 mm |
| SP6 | X | 73,6543 mm |
| SP6 | Y | 117,4445 mm |
| SP7 | X | 160,9931 mm |
| SP7 | Y | 92,429 mm |
| SP8 | X | 44,849 mm |
| SP8 | Y | 83,8384 mm |
Schritt 1:
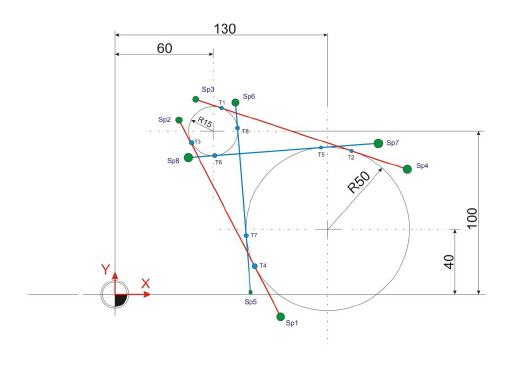
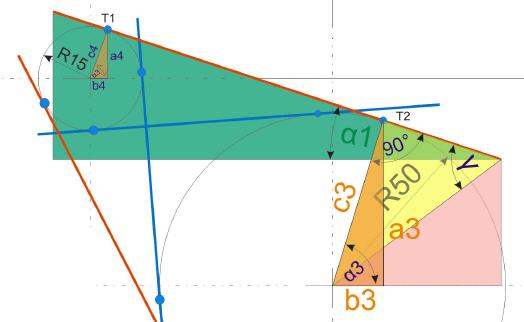
Es spielt keine Rolle, welchen Berührpunkt man zuerst berechnet. In diesem Fall werden zunächst die Berührpunkte aus derjenigen Geraden berechnet, die sich aus den Punkten Sp3 und Sp4 ergibt.
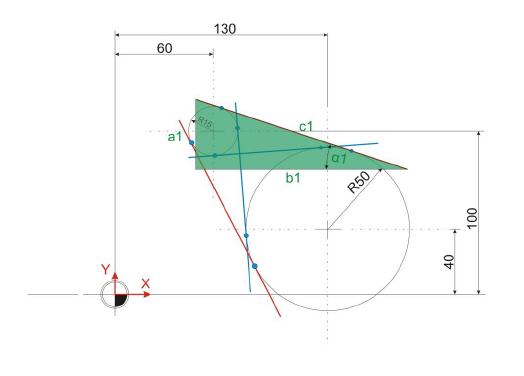
Im ersten Schritt der Berechnung der beiden Berührpunkte ist es nötig, die Strecke c der Hypotenuse des grünen Dreiecks zu ermitteln. Dieses Dreieck wird aus dem Start- beziehungsweise Endpunkt der Geraden gebildet, die sich als
Tangente an die zwei Kreise anschmiegt.
Der Winkel Alpha diese Dreiecks ist wie folgt zu ermittel:
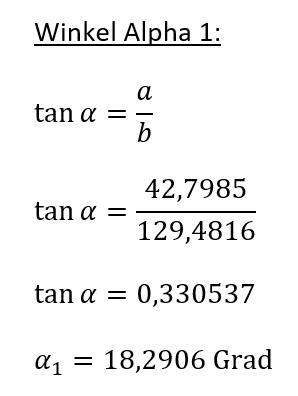
Schritt 2:
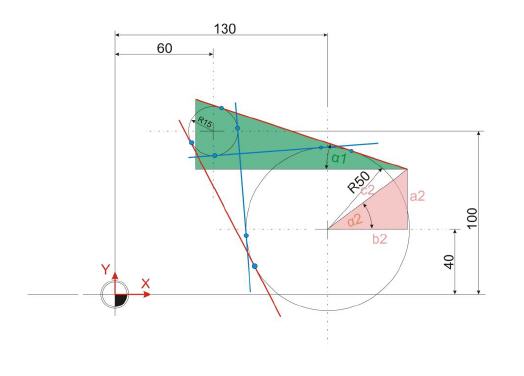
Nun wird der Winkel Alpha 2 sowie die Strecke c2
ermittelt.
Der Rechenweg lautet:

Schritt 3:
Für den dritten Schritt ist die Erkenntnis wichtig,
dass der Winkel Beta durch die im schiefwinkligen
Dreieck liegende Gerade c mit der Tangende bildet.
Diese ergeben einen 90-Grad-Winkel.
Somit muss nur noch der Winkel Alpha berechnet
werden, da der Winkel Gamma ebenfalls bekannt ist.
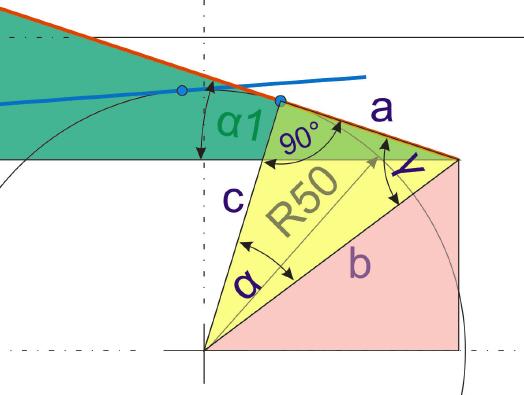
Der Rechenweg lautet:
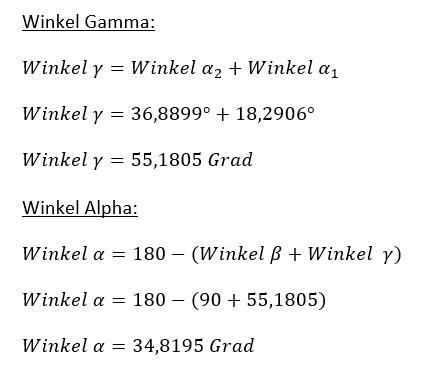
Die Strecke c im schiefwinkligen muss nicht berechnet
werden, da sich diese aus dem Radius des Kreises
ergibt. Somit gilt:
c=R
c= 50mm
Schritt 4:
Nun ist es möglich, die Koordinaten der Berührpunkte zu berechnen. Festzuhalten ist nur, dass der Winkel Alpha 3 sich aus dem Winkel Alpha 2 sowie dem Winkel Alpha des schiefwinkligen Dreiecks zusammensetzt.
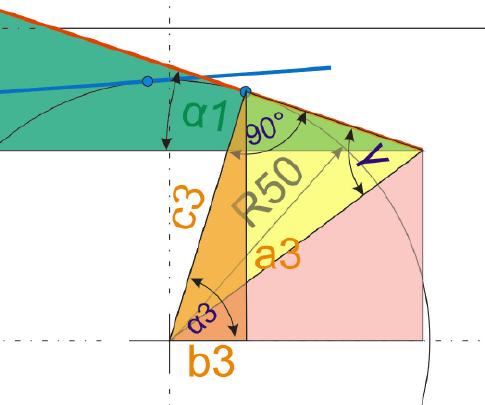
Der Rechenweg lautet:
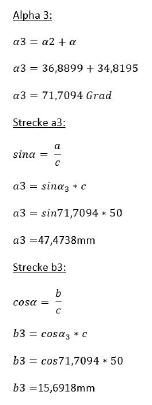
Schritt 5:
Nun kann problemlos der Berührpunkt
auf dem anderen Kreis berechnet werden.
Das geht sehr rasch, da nun der dazu
nötige Winkel bekannt ist: Alpha 3.
Der Rechenweg lautet:
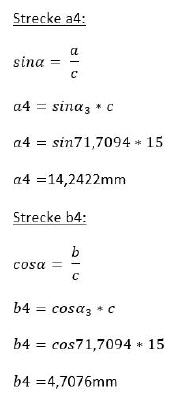
Schritt 5:
Als letzten Schritt gilt es nur mehr, die Koordinaten der berechneten Punkte korrekt vom Nullpunkt aus zu bestimmen.
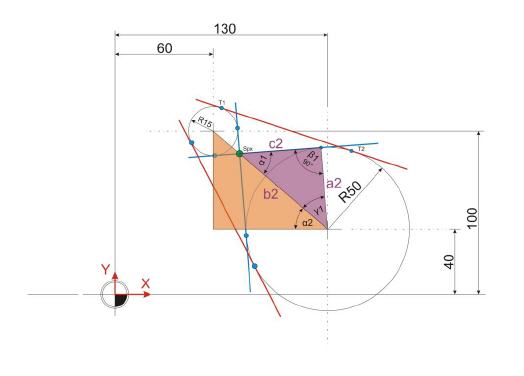
Tangente T1:
T1-X=60+4,7076=64,7076mm
T1-Y=100+14,2422=114,2422mm
Tangente T2:
T2-X=130+15,6918=145,6918mm
T2-Y=40+47,4738=87,4838mm
Nach diesem Schema lassen sich nun alle Berührpunkte der Tangenten bestimmen.
Kleine Abweichungen kommen durch Rundungsfehler zustande. Daher immer mit voller Rechengenauigkeit arbeiten.
Die Alternative:
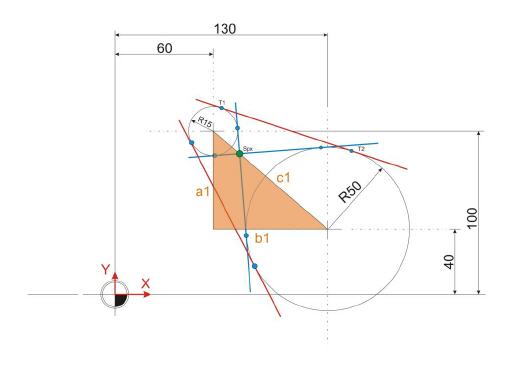
Häufig sind keine Start- und Endpunkte der Geraden bekannt. In diesem Fall muss ein anderer Weg beschritten werden, um die Berührpunkte von Tangenten zu berechnen.
Schritt 1:
Zunächst gilt es, den Abstand der beiden Kreise zu bestimmen, der durch die Strecke c1 repräsentiert wird.
Der Rechenweg lautet:
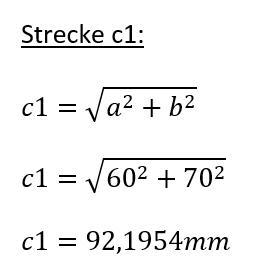
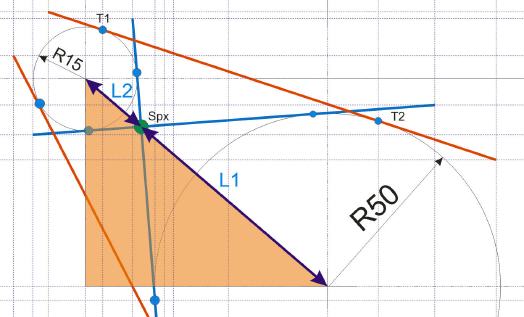
Nun wird der Punkt SPx wichtig. Dieser Punkt bildet sich als Schnittpunkt zwischen den blau eingefärbten Tangenten aus. Er steht im Verhältnis zu den Durchmessern der beiden Kreise. Besitzen die Kreise den gleichen Durchmesser, so befindet sich dieser Punkt genau in der Mitte des Abstands der beiden Kreise. Jede Änderung des Durchmessers verändert daher die Lage des Punktes SPx entlang der Strecke c.
Größenverhältnis der Kreise

Der große Kreis ist demnach um dieses Verhältnis größer, als der kleine Kreis. Dies bedeutet, dass die Strecke c so aufzuteilen ist, dass diejenige Strecke, die vom Kreismittelpunkt des großen Kreises ausgeht, um dieses Verhältnis länger sein muss, als die Strecke des kleinen Kreises. Dazu muss nur die Zahl 1 zum Wert 3,3333 addiert werden, denn dies ist das auf die Länge von c1 übertragene Längenverhältnis, das 100 Prozent entspricht. 4,33333 entsprechen also 100 Prozent. 3,3333 demnach 76,923 Prozent. Die Länge der Strecke c1 wird demnach entsprechend der Größenverhältnisse zwischen kleinem und großen Kreis aufgeteilt.
Berechnung:
4,33333 = 100
1= 100/4,3333
3,3333=100/4,3333*3,3333=76,923%
Schritt 2:
Wenn die Durchmesser beider Kreise identisch wären, dann würde die Länge von c1 exakt hälftig geteilt werden. Der Punkt Spx wäre dann von beiden Kreismittelpunkten gleich weit entfernt.
Da jedoch der große Kreis 3,3333 mal so groß ist, wie der kleine Kreis, wird die Strecke c1 wie folgt aufgeteilt:
100% = 92,1954mm
L1 = 76,923% = 70,9195mm
L2 = 92,1954-70,9195 = 21,2759mm
Mit diesen Angaben ist es nun möglich, die beiden Winkel Alpha1 und Gamma1 zu berechnen. Zu beachten ist lediglich, b2 gleich L1 entspricht.
Der Winkel Alpha 1 errechnet sich wie folgt:
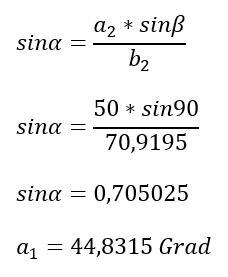
Der Winkel Gamma1 kann nun sehr einfach durch Subtrahieren der beiden bekannten Winkel von 180 Grad ermittelt werden.
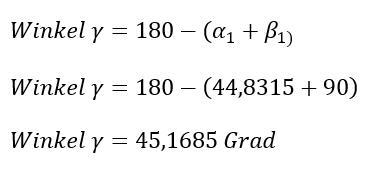
Der Winkel Alpha 2 kann auch gleich ermittelt werden, da dieser zur Berechnung des nächsten Winkels benötigt wird.
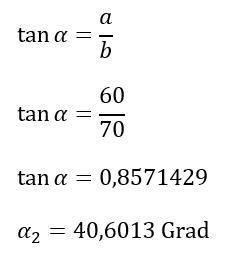
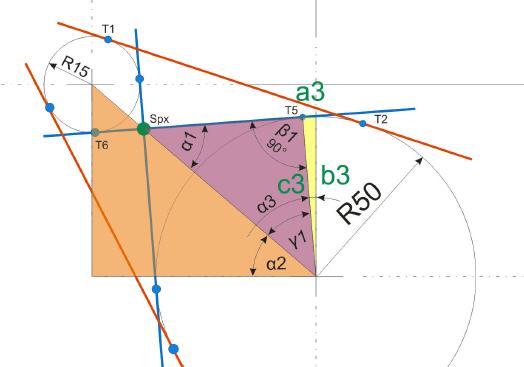
Schritt 3:
Nun ist der Weg frei, die Koordinaten für Punkt T5 zu berechnen. Dazu muss lediglich noch der Winkel Alpha 3 sowie die Strecken a3 und b3 berechnet werden.
Winkel Alpha 3
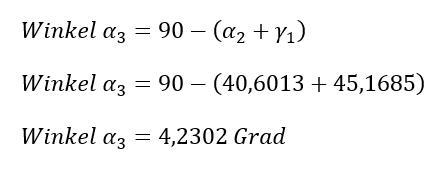
Strecke a3
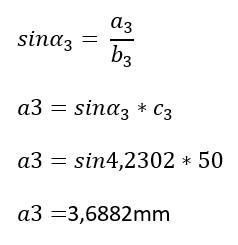
Strecke b3
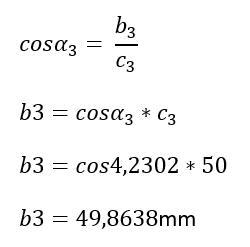
Die Koordinaten des Punktes T5 können bestimmt werden, nachdem die Strecken a3 und b3 bekannt sind:
T5-X=130-3,6882
T5-X=126,3118mm
T5-Y=40+49,8638
T5-Y=89,8638mm
Schritt 4:
Zur Berechnung des Punktes T7 ist nur mehr eine Wiederholung der vorhin getätigten Berechnungen nötig. Allerdings ist darauf zu achten, dass nun unter Umständen andere Formeln zur Anwendung kommen, wenn das schiefwinklige Dreieck entsprechend neu platziert wird.
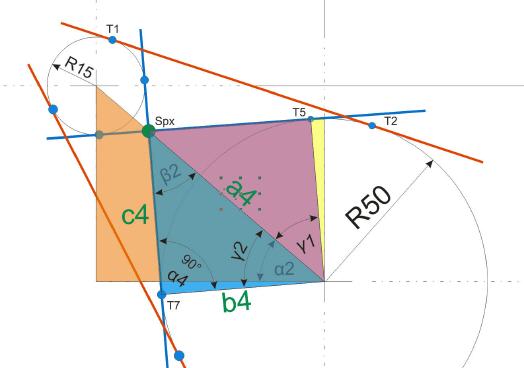
Winkel Beta 2 berechnen:
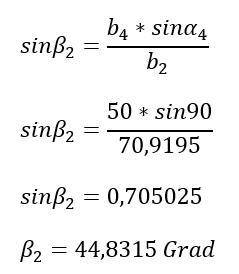
Der Winkel Gamma2 kann nun sehr einfach durch Subtrahieren der beiden bekannten Winkel von 180 Grad ermittelt werden.
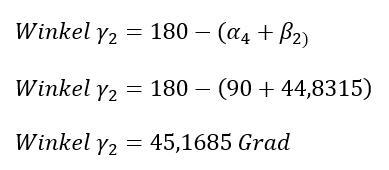
Nun ist es nur mehr ein kurzer Weg. Um die Koordinaten des Punktes T7 berechnen zu können. Dazu ist zunächst der Winkel Alpha5 zu berechnen, der sich sehr einfach durch Subtrahieren des Winkels Alpha2 vom Winkel Gamma2 berechnen lässt.
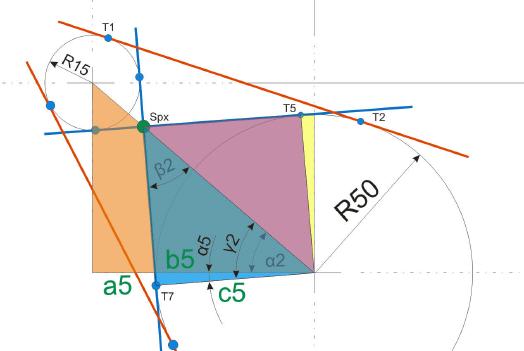
Winkel Alpha 5 berechnen:
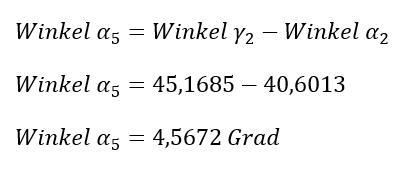
Strecke a5 berechnen:
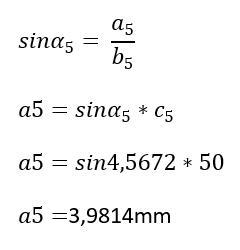
Strecke b5 berechnen:
Die Koordinaten des Punktes T7 können bestimmt werden, nachdem die Strecken a5 und b5 bekannt sind:
T7-X=130-49,8412
T7-X=80,1588mm
T7-Y=40-3,9814
T7-Y=36,0186mm
Die Tangentenpunkte des kleinen Kreises werden auf identische Weise berechnet. Hierzu soll jeder selbst die Lösung finden. Die Ergebnisse lauten:
T6-X=61,1065mm
T6-Y=85,0409mm
T8-X=74,9524mm
T8-Y=101,1944mm
Download:
Zu diesem Artikel können Sie hier eine Excel-Tabelle zur Berechnung von Tangente-Kreis-Kreis herunterladen [1.303 KB] .
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 5 - gesamt: 4368.
















































































