Schnittpunktberechnung Gerade-Kreis
Geometrische Probleme rasch gelöst
Die Dreiecksberechnung zu beherrschen bedeutet, künftig viele Berechnungen geometrischer Art problemlos durchführen zu können. Wenn eine Gerade einen Kreis schneidet, ist es damit eine Leichtigkeit, die Lage der beiden Durchdringungspunkte zu ermitteln.
Bevor dieses Manuskript durchgearbeitet wird, empfiehlt sich die Lektüre des Artikels ›Berechnung der Schnittpunkte zwischen zwei Kreisen‹, der hier zu finden ist. Erst mit dieser Grundlage kann an dieser Stelle sinnvoll weitergelesen werden, da sonst wesentliche Dinge unbekannt bleiben. Beispielsweise wird dort umfassend erklärt, wie das schiefwinklige Dreieck handzuhaben ist und sich dessen Strecken und Winkel berechnen lassen.
Wie hinreichend bekannt, führen immer mehrere Wege ans Ziel. Das gilt nicht nur für Wanderer, sondern auch für Fans der Mathematik. Nicht alle Wege sind für jeden gleichermaßen geeignet, da für die Art und Weise, wie mathematische Probleme gelöst werden, jeder andere Vorlieben hat, wenn sich mehrere Lösungswege anbieten. Der folgende Lösungsweg zum Berechnen der beiden Schnittpunkt, die sich beim Durchdringen einer Geraden durch einen Kreis ergeben, ist daher nicht unbedingt jedermanns Favorit, doch kommt er den Fachleuten entgegen, die nicht am Gymnasium Mathe hatten und daher schwerpunktmäßig die Dreiecksberechnung zur Lösung geometrischer Aufgaben heranziehen.
Schritt 1:
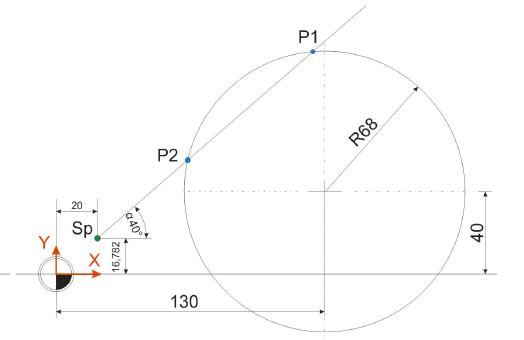
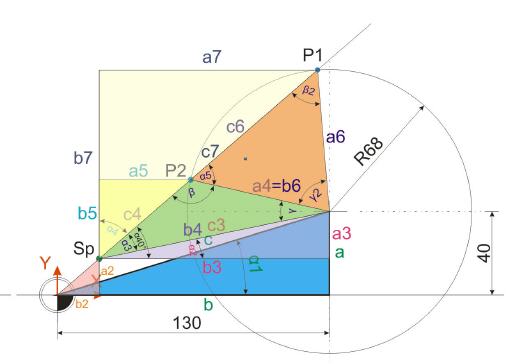
Im ersten Schritt der Schnittpunktsberechnung ist es nötig, den Winkelwert Alpha 1 sowie die Strecke c der Hypotenuse des blauen Dreiecks zu ermitteln. Die Ankathete a (40 mm) sowie die Gegenkathete b (130 mm) sind bekannt und werden für diese Berechnungen herangezogen.
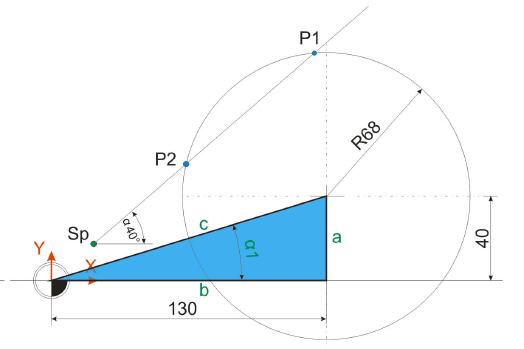
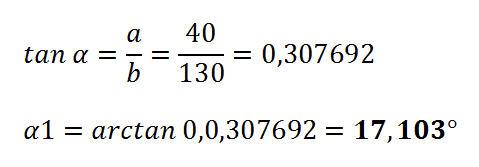
Die Länge der Strecke c, also der Geraden zwischen dem Null- und dem Kreismittelpunkt, ist wie folgt zu ermittel:
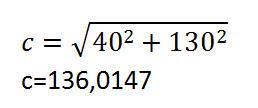
Schritt 2:
Im zweiten Schritt geht es darum, Strecken zu ermitteln, die zur Bildung eines schiefwinkligen Dreiecks führen, mit dem sich dann die Lage von Punkt P2 ermitteln lässt. Zur besseren Übersicht werden zunächst die Punkte aufgeführt , die bereits bekannt sind.
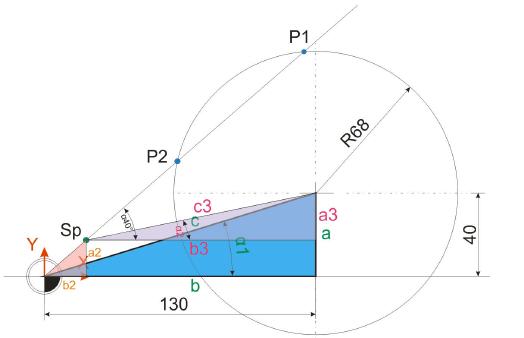
a2=16,782mm
b2=20mm
Strecke a3:
a3=40-a2
a3=40-16,782
a3=23,218mm
Strecke b3:
b3=130-b2
b3=130-20
b3=110mm
Strecke c3:
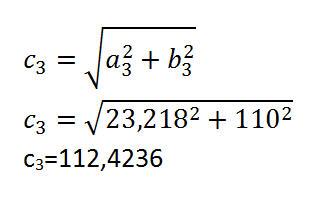
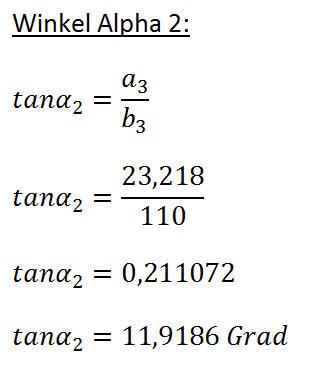
Schritt 3:
Im dritten Schritt wird der Winkel Alpha 3 berechnet. Die Berechnung dieses Winkels ist einfach, da hier nur der Winkel Alpha 2 vom bereits bekannten Winkel der Geraden abzuziehen ist.
Alpha 3 = 40° - Alpha 2
Alpha 3 = 40° - 11,9186°
Alpha 3 = 28,0814 Grad
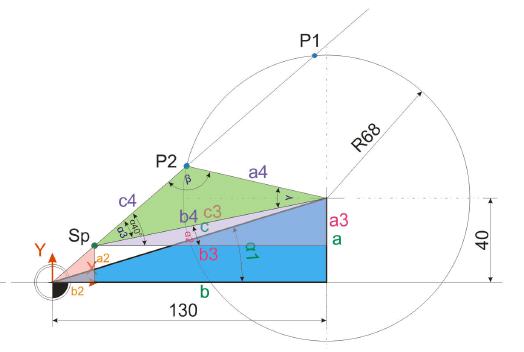
Da nun drei Werte des schiefwinkligen Dreiecks bekannt sind, nämlich die Strecken b4 beziehungsweise c3 (136,0147mm) und a4 (R68mm) sowie der Winkel Alpha3, kann der Winkel Beta berechnet werden.
Da der Winkel Beta größer als 90 Grad ist, lautet die Formel:
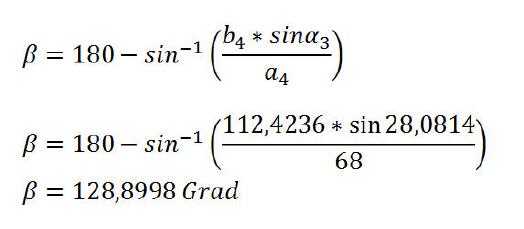
Info: sin-1 (Arcussinus) ist die Umkehrfunktion der Sinusfunktion.
Der Winkel Gamma kann nun einfach durch die Subtraktion der beiden jetzt bekannten Winkel ›Alpha 3‹ sowie ›Beta‹ von der Winkelsumme 180 Grad ermittelt werden:
Gamma= 180-(Alpha 3 + Beta)
Gamma= 180-(28,0814 + 128,9)
Gamma= 23,0188 Grad
Nun ist es möglich, die Strecke C4 zu berechnen. Die Formel dazu lautet:
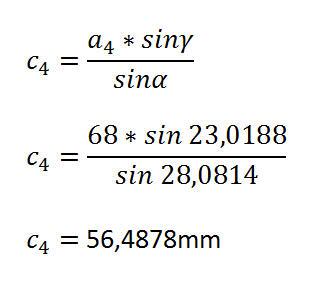
Wer mit dem Taschenrechner einen anderen Wert bekommen hat: Dies ist die Folge von Rundungsfehlern. Daher immer darauf achten, stets die volle Genauigkeit des Taschenrechners zu nutzen.
Schritt 4:
Nachdem nun die Strecke C4 bekannt ist, kann die Lage des Punktes P2 problemlos ermittelt werden. Dazu wird zunächst der Winkel Alpha 4 ermittelt.
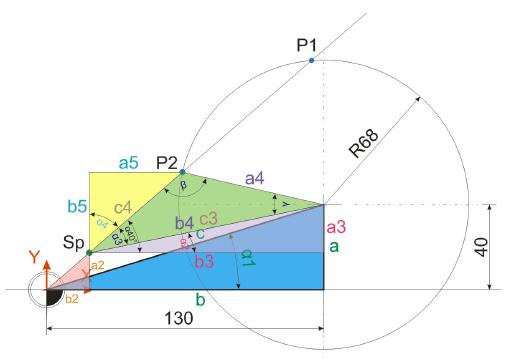
Alpha 4 = 90 Grad – Alpha
Alpha 4 = 90° – 40°
Alpha 4 = 50°
Nachdem nun der Winkel dieses Dreiecks bekannt ist, können die beiden Strecken a5 und b5 ermittelt werden.
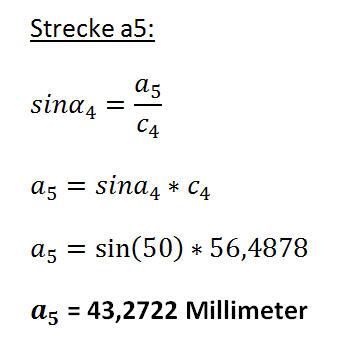
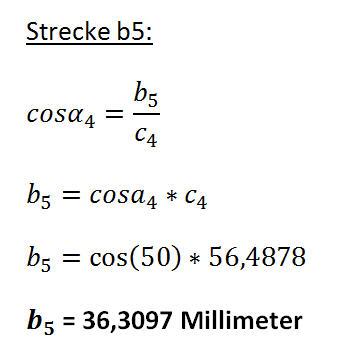
Mit diesen Werten wird es nun möglich, die Koordinaten des Punktes P2 zu bestimmen.
P2-X= b2+a5
P2-X= 20+43,2722
P2-X= 63,2722mm
P2-Y= a2+b5
P2-Y= 16,782+36,3097
P2-Y= 53,0917mm
Schritt 5:
Um Punkt P1 berechnen zu können, muss zunächst klar herausgestellt werden, dass das schiefwinklige Dreieck eine völlig neue Position eingenommen hat. Dies hat zur Folge, dass sich der Betrachter genau überlegen muss, wo
die Winkel Alpha, Beta und Gamma liegen. Entsprechend müssen auch die Strecken a, b und c festgelegt werden. Wird dies nicht beachtet, werden Rechenvorgänge zu falschen Ergebnissen führen.
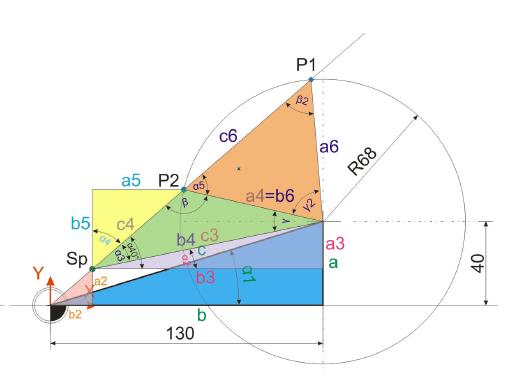
Zunächst wird einmal festgehalten, was schon alles bekannt ist:
Strecke a6 = 68mm
Strecke b6=68mm
Winkel Alpha5=180°-128,9°=51,1°
Nun ist es noch nötig, die Winkel Beta2 und Gamma2 zu berechnen.
Winkel Beta 2:
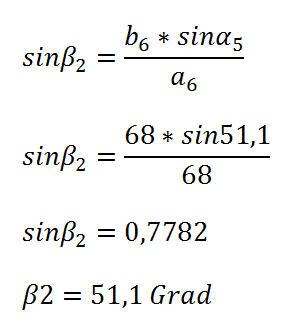
Der Winkel wird ermittelt, indem die Umkehrfunktion des Sinus eingesetzt wird. Sin-1 0,7782=51,1°
Nachdem nun zwei Winkel im schiefwinkligen Dreieck bekannt sind und die Winkelsumme stets 180 Grad ergibt, kann der dritte, fehlende Winkel einfach berechnet werden:
Gamma 2 = 180 – (Beta 2 + Alpha 5)
Gamma 2 = 180° – (51,1° + 51,1°)
Gamma 2 = 77,8 Grad
Mit der Ermittlung von Winkel Gamma 2 ist der Weg frei für die Berechnung der Geraden c6, die zur Koordinatenermittlung des Punktes P1 noch fehlt.
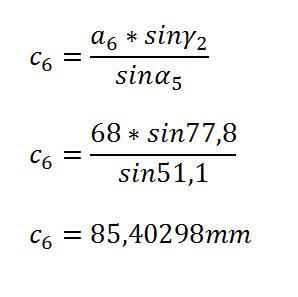
Schritt 6:
Nachdem nun die Strecke c6 bekannt ist, können die Koordinaten des Punktes P1 ermittelt werden. Dazu wird zunächst die Strecke c7 ermittelt, die sich aus den Strecken c4 und c6 zusammensetzt.
Strecke c7:
c7=c4+c6
c7=56,4878+85,403
c7=141,8908mm
Strecke a7:
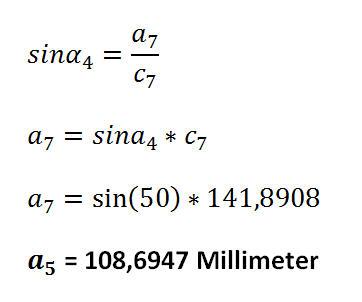
Strecke b7:
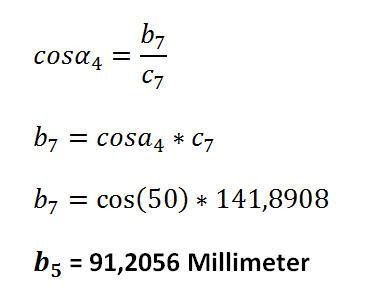
Mit diesen Werten wird es nun möglich, die Koordinaten des Punktes P1 zu bestimmen.
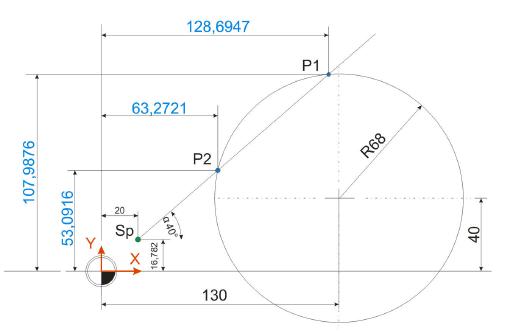
P1-X= b2+a7
P1-X= 20+108,6947
P1-X= 128,6947mm
P1-Y= a2+b7
P1-Y= 16,782+91,2056
P1-Y= 107,9876mm
Download:
Eine Excel-Tabelle zum Berechnen der Schnittpunkte zwischen Kreis und Gerade können Sie hier herunterladen [725 KB] .
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 3 - gesamt: 1985.
















































































