Punktberechnung Kreismittelpunkt und Radius
Mit zwei und drei Punkten zum Kreis
Zwei Punkte reichen bereits, um einen Kreis zu beschreiben. Die Berechnung des sich ergebenden Kreisradius sowie des Kreismittelpunktes ist hier relativ einfach. Mehr Überlegung ist nötig, wenn ein dritter Punkt hinzukommt. Aber auch dies lässt sich leicht lösen, wenn man konsequent dem Weg des Dreiecks folgt.
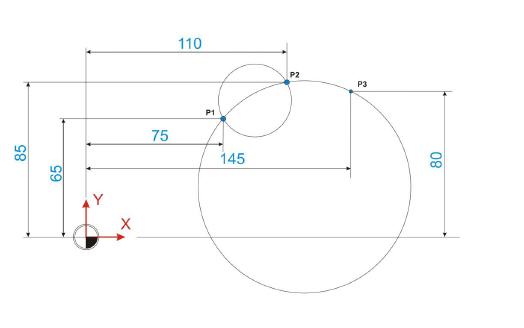
Wie bereits bei den vorhergehenden Kursen angesprochen, gilt auch diesmal folgender Rat: Bevor dieses Manuskript durchgearbeitet wird, empfiehlt sich die Lektüre des Abschnitts ›Berechnung der Schnittpunkte zwischen zwei Kreisen‹. Erst mit dieser Grundlage kann an dieser Stelle sinnvoll weitergelesen werden, da sonst wesentliche Dinge unbekannt bleiben.
Folgende Beschreibung erhebt keinen Anspruch, den besten Rechenweg zur Berechnung von Radius und Kreismittelpunkt zu beschreiben, wenn zwei oder drei Punkte gegeben sind. Wie hinreichend bekannt, führen immer mehrere Wege ans Ziel. Nicht alle Wege sind jedoch für jeden gleichermaßen geeignet. Der vorgeschlagene Lösungsweg ist daher nicht unbedingt jedermanns Favorit. Er kommt jedoch den Fachleuten entgegen, die gerne die Dreiecksberechnung zur Lösung geometrischer Aufgaben heranziehen.
Kreisradius und Kreismittelpunkt aus zwei Punkten
Im ersten Schritt der Berechnung des Kreisradius ist es nötig, die Strecke c der Hypotenuse des orangen Dreiecks zu ermitteln. Der Radius ergibt sich dann durch einfaches halbieren des Ergebnisses. Die Ankathete a (20 mm) sowie die Gegenkathete b (35 mm) sind bekannt und werden für diese Berechnungen herangezogen.
Die Länge der Strecke c, also der Geraden zwischen den beiden Punkten, ist wie folgt zu ermittel:
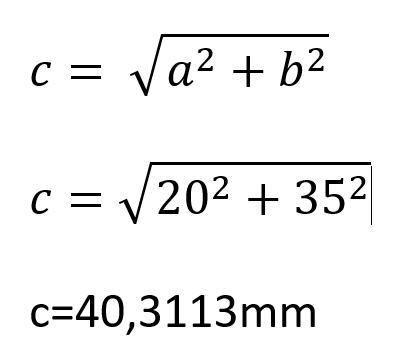
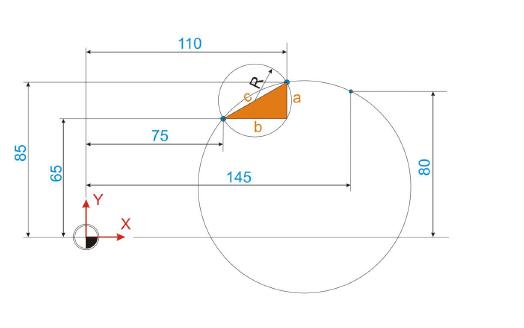
Der gesuchte Radius ist folglich das Ergebnis aus: 40,3113/2=20,1556mm
Der Kreismittelpunkt Pa ist rasch ermittelt, da sich dieser aus den Mittelspunktskoordinaten der beiden bekannten Punkte ergibt. Je nachdem, welcher Punkt verwendet wird, müssen Plus- oder Minusrechnungen angestellt werden.
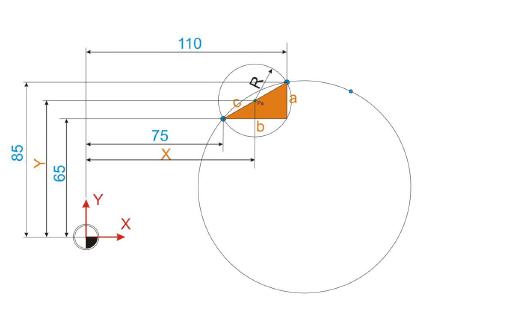
Musterlösung:
X = 75 + b/2
X= 75 + 35/2
X= 92,5mm
Y = 65 + a/2
Y = 65 + 20/2
Y = 75mm
Kreisradius und Kreismittelpunkt aus drei Punkten
Schritt 1:
Wenn drei Punkte gegeben sind, kann der Umkreismittelpunkt aus der Tatsache berechnet werden, dass die im 90-Grad-Winkel von den Hypotenusen abgehenden Geraden sich an einem gemeinsamen Punkt treffen, der den Mittelpunkt des durch die drei Punkte gehenden Kreises bildet.
Der Punkt, an dem die Geraden jeweils ausgehen, kann besonders einfach errechnet werden. Dazu ist nur jeweils der Wert der Ankathete a sowie der Gegenkathete b zu halbieren und das Ergebnis entsprechend des gewählten Startpunkts vom diesem zu addieren oder zu subtrahieren.
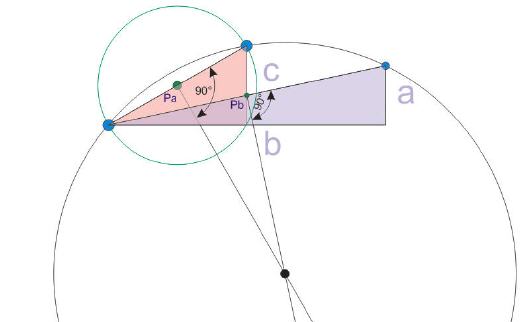
Punkt Pa:
Dieser Punkt wurde bereits berechnet.
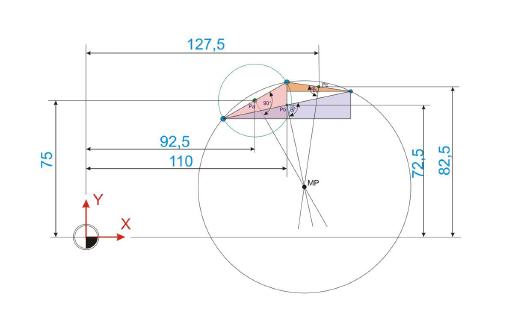
Pa-X = 92,5mm
Pa-Y = 75mm
Punkt Pb:
a = 80-65 = 15mm
b = 145-75 = 70mm
Pb-X = 75+70/2 = 110mm
PB-Y = 65+15/2 = 72,5mm
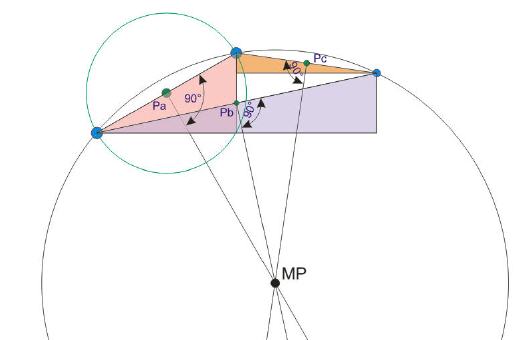
Punkt Pc:
a = 85-80 = 5mm
b = 145-110 = 35mm
Pc-X = 110+35/2 = 127,5mm
Pc-Y = 80+5/2 = 82,5
Schritt 2:
Nachdem nun die Punkte berechnet wurden, kann mit einem Winkel von jedem Punkt aus eine Linie zum vermuteten Kreismittelpunkt gezogen werden. Dort, wo sich alle Linien treffen, ist der exakte Mittelpunkt des Kreises, der durch alle vorgegebenen Punkte hindurchläuft. Doch wie wird die berechnet?
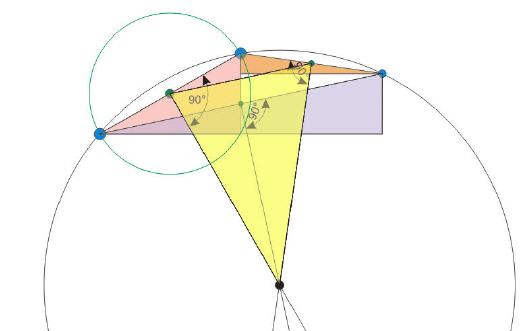
Zur exakten Berechnung des Kreismittelpunktes ist es zunächst nötig, die Winkel von mindestens zwei zueinanderstehenden Geraden zu ermitteln. Dazu werden die Winkel Beta und Gamma ermittelt. Um zunächst den Winkel Beta zu ermitteln, sind die Winkel W1 und W2 zu berechnen.
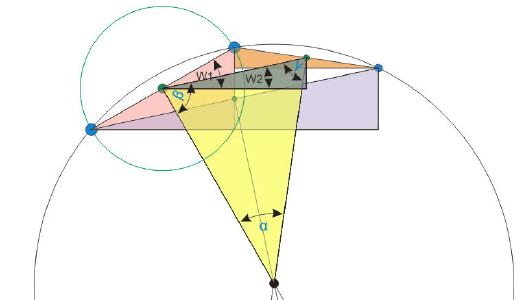
Winkel W1:
tanα=a/b=10/17,5=0,57143
w1=29,7449°
Winkel W2:
tanα=a/b=7,5/35=0,2142857
w2=12,09476°
Winkel Beta wird danach durch einfaches
Subtrahieren der beiden eben errechneten
Winkel bestimmt.
Winkel Beta:
Winkel Beta = 90°-(W1-W2)
Winkel Beta = 90°-(29,7449-12,09476)
Winkel Beta = 72,3499 Grad
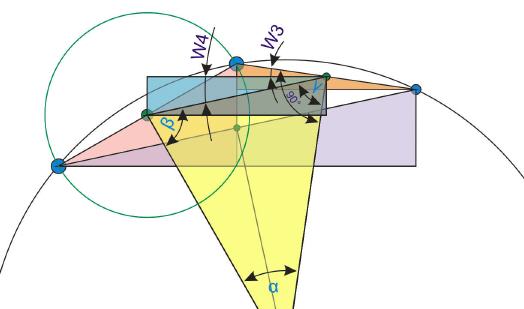
Der Winkel Gamma wird auf die gleiche Weise ermittelt. Auch diesmal werden zwei Hilfswinkel ermittelt, mit deren Hilfe sich der Winkel Gamma ermitteln lässt.
Winkel W3:
tanα=a/b=2,5/17,5=0,142857
w3=8,1301°
Winkel W4:
tanα=a/b=7,5/35=0,214286
w3=12,09476°
Winkel Gamma kann danach durch einfaches Subtrahieren der beiden eben errechneten Winkel bestimmt werden.
Winkel Gamma:
Winkel Gamma = 90°-W3-W4
Winkel Gamma = 90-8,1301-12,09476
Winkel Gamma = 69,7751 Grad
Winkel Alpha:
Nachdem nun die beiden Winkel berechnet sind, kann der letzte Winkel in diesem Dreieck sehr einfach ermittelt werden: Da die Winkelsumme im Dreieck stets 180 Grad ist, müssen von dieser Winkelsumme nur die beiden Winkel Beta und Gamma subtrahiert werden, um den Winkel Alpha zu erhalten.
Winkel Alpha = 180°-Winkel Beta-Winkel Gamma
Winkel Alpha = 180°-72,3499°-69,7751°
Winkel Alpha = 37,875 Grad
Schritt 3:
Die nun vorliegende Ergebnisse ermöglichen es, die fehlenden Werte im schiefwinkligen Dreieck, nämlich die Strecke a und c zu ermitteln. Die gesuchten Werte im schiefwinkligen Dreieck wurden mit roten Buchstaben gekennzeichnet, damit es keine Verwechslung mit den dunkelblau ausgelegten Buchstaben zur Berechnung der Strecke a kommt.
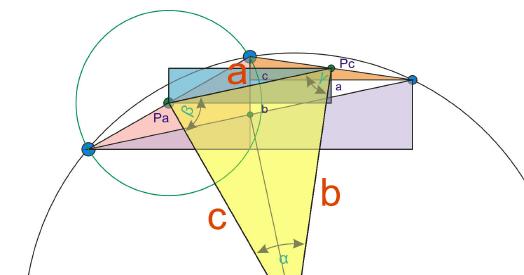
Strecke a:
Die Länge der Strecke a ist das Ergebnis der Berechnung der Hypotenuse c, die sich als Linie zwischen den Punkten Pa und Pc ergibt.
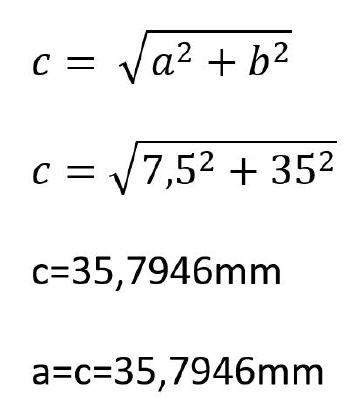
Strecke c:
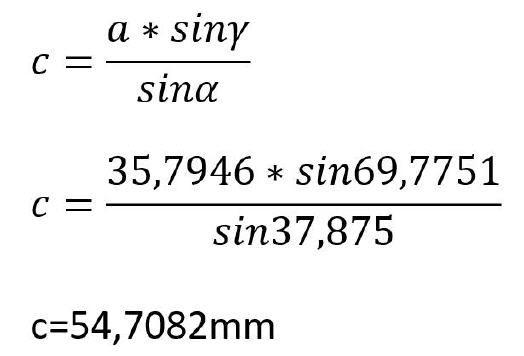
Die Strecke b ist eigentlich für die weiteren Berechnungen nicht nötig, dennoch soll sie hier zum Verständnis der Berechnungen im schiefwinkligen Dreieck aufgeführt werden.
Strecke b:
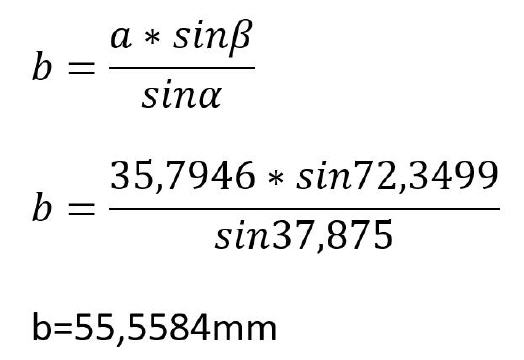
Schritt 4:
Nachdem nun auch die Maße des das schiefwinkligen Dreiecks ermittelt wurden, können endlich die Koordinaten des Kreismittelpunkts berechnet werden. Dazu wird ein rechtwinkliges Dreieck von Punkt Pa zum Kreismittelpunkt gelegt und die Strecken a und b berechnet. Damit dies möglich ist, muss jedoch zunächst der Winkel Alpha 2 ermittelt werden.
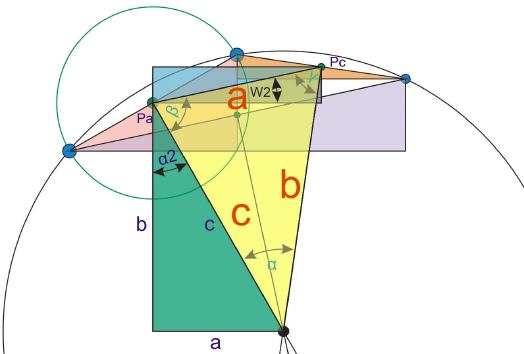
Alpha 2:
Alpha 2 = 90° - (Winkel Beta – Winkel W2)
Alpha 2 = 90° - (72,3499 – 12,09476)
Alpha 2 = 29,74486 Grad
Ankathete a:
sinα=a/c
a=sinα*c
a=sin29,74486*54,7082
a = 27,1429mm
Gegenkathete b:
cosα=b/c
b=cosα*c
b=cos29,74486*54,7082
b = 47,5mm
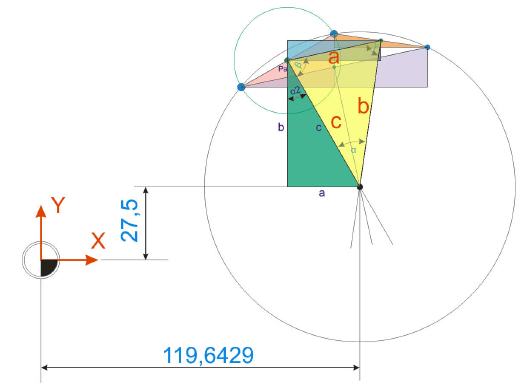
Nachdem nun alle Maße ermittelt sind, kann der Kreismittelpunkt berechnet werden. Dazu werden die berechneten Werte einfach mit den Koordinaten des Punktes Pa entsprechend verarbeitet.
Kreismittelpunkt X:
KMP-X = Pa-X + a
KMP-X = 92,5 + 27,1429
KMP-X = 119,6429mm
Kreismittelpunkt Y:
KMP-Y = Pa-Y – b
KMP-Y = 75 – 47,5
KMp-Y = 27,5mm
Download:
Eine Excel-Tabelle zum Berechnen des Kreismittelpunktes aus drei gegebenen Punkten können Sie hier im XLSX-Format herunterladen [1.232 KB] .
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 2 - gesamt: 49637.
















































































