Schnittpunktberechnung Kreis-Kreis
Das schiefwinklige Dreieck in der Praxis
Wer die Dreiecksberechnung beherrscht, hat künftig keine Probleme mehr, selbst anspruchsvolle geometrische Fälle zu lösen. Wenn sich beispielsweise zwei Kreise schneiden, ist durch die Anwendung der Dreiecksberechnung die Berechnung der Lage beider Schnittpunkte rasch erledigt.
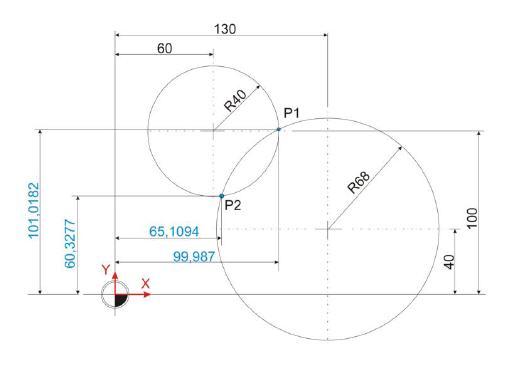
Viele Wege führen nach Rom. Diese Erkenntnis ist auch für das Fach Mathematik eine wichtige Erkenntnis. Das nun folgende Beispiel ist lediglich als Musterlösung zu verstehen, die Schnittpunkte zweier sich durchdringender Kreise zu berechnen. Diese Schnittpunkte sind auf mehreren Wegen ermittelbar. Wer dir folgende Musterlösung verstanden hat, ist herzlich eingeladen, die Schnittpunkte auf alternative Weise zu berechnen, um so sein Verständnis für geometrische Berechnungen zu trainieren.
Viele Problemstellungen der Geometrie sind bereits durch die alleinige Anwendung des rechtwinkligen Dreiecks zu lösen. Die Formel dazu lautet:
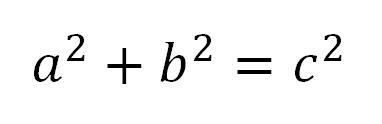
Durch Umstellen dieser Formel lassen sich alle gesuchten Bestandteile des rechtwinkligen Dreiecks einfach aus den bekannten Bestandteilen ermitteln. So ermittelt man beispielsweise die Strecke c mit dieser Formel:
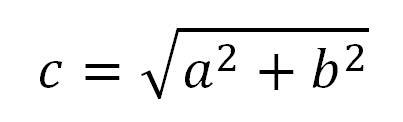
Kommen Winkel hinzu, so wird die zweite Stufe der Dreiecksberechnung gezündet: Nun kommt die Trigonometrie ins Spiel. Um diese Wort wird unnötigerweise oft eine mystische Mathe-Welt aufgebaut. Dabei geht es hier lediglich darum, Verhältniswerte zwischen den Längen zweier Seiten des betrachteten Dreiecks zu ermitteln und aus diesem Wert wiederum den gesuchten Winkel zu errechnen.
Die wichtigsten trigonometrischen Formeln lauten:
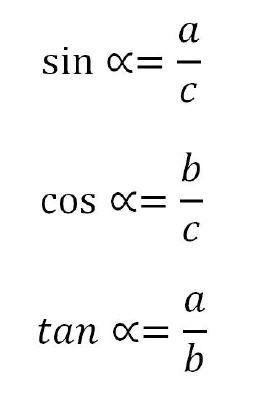
Die Zusammenhänge bezüglich der Berechnung eines rechtwinkligen Dreiecks wurde in der online-Ausgabe der Welt der Fertigung bereits ausführlich behandelt. Der Kurs findet sich hier. Dieser sollte unbedingt durchgearbeitet werden, um bei der dritten Stufe der kommenden Dreiecksberechnung nicht auszusteigen.
Das schiefwinklige Dreieck
Wer das Rechnen im schiefwinkligen Dreieck beherrscht, der ist aller Sorgen entledigt, wenn am gegeben Dreieck kein rechter Winkel vorhanden ist. Im Grunde verändert sich die Handhabung und das Verständnis zur Dreiecksberechnung nicht. Die Summe aller Winkel ist nach wie vor 180 Grad und auch hier ist ein Verhältnis der Winkel und Strecken untereinander die Grundlage, um die gesuchten Werte beziehungsweise Winkel zu ermitteln. Was sich allerdings ändert, sind die Formeln, die ein klein wenig umfangreicher ausfallen, um jede Fragestellung zum schiefwinkligen Dreieck zu beantworten.

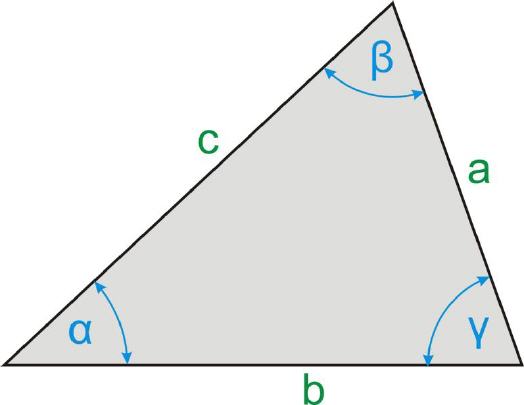
Diese Formeln müssen nun umgestellt werden, sollen Winkel berechnet werden. Es sind sowohl der Sinussatz, als auch der Cosinussatz nutzbar. Welche Formel verwendet werden kann, hängt immer davon ab, welche Daten gegeben sind.
Winkel Alpha berechnen:
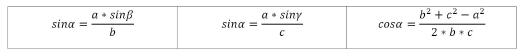
Winkel Beta berechnen:
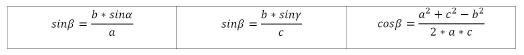
Wenn Beta > 90°, dann gelten diese Formeln:
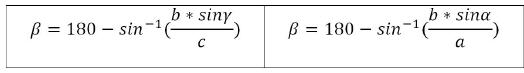
Winkel Gamma berechnen:
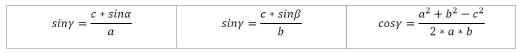
Sind hingegen die Seiten gesucht, so müssen die Formeln wiederum anders umgestellt werden.
Berechnung der Seite a:

Berechnung der Seite b:

Berechnung der Seite c:

Berechnung der Fläche:
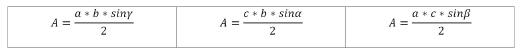
Schnittpunkte von zwei sich schneidenden Kreisen:
Wie bereits erwähnt, gibt es mehrere Möglichkeiten, die Schnittpunkte von zwei sich schneidenden Kreisen zu berechnen. Der hier vorgestellte Weg handelt von der Schnittpunktermittlung unter der Anwendung des rechtwinkligen sowie des schiefwinkligen Dreiecks.

Schritt 1:
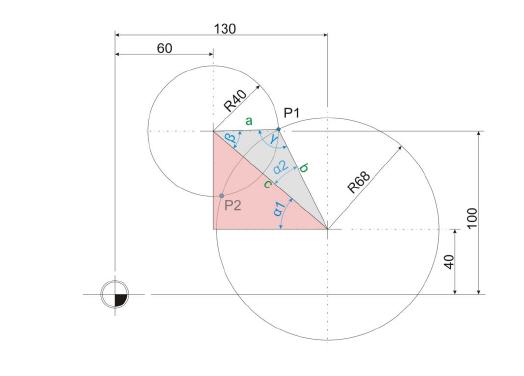
Im ersten Schritt der Schnittpunktsberechnung ist es nötig, den Winkelwert Alpha 1 zu ermitteln , den die gedachte Gerade zwischen den beiden Mittelpunkten der Kreise bezogen auf die waagrechte X-Achse einnimmt. Da sich hier ein rechtwinkliges Dreieck bildet, ist die Berechnung rasch erledigt.
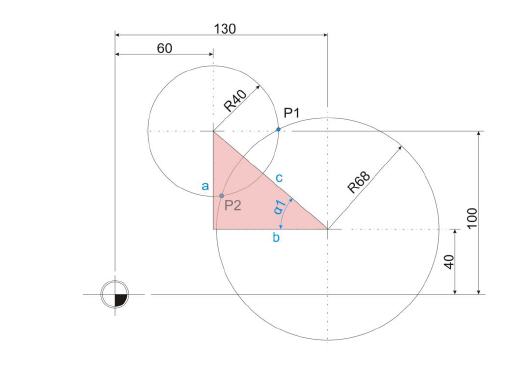
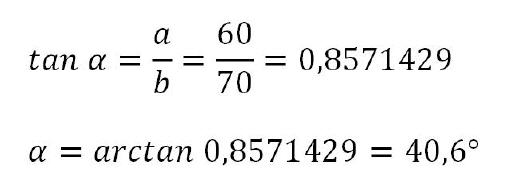
Die Strecke C, also die direkte Gerade zwischen
Kreismittelpunkt 1 und Kreismittelpunkt 2,
ist wie folgt zu ermittel:
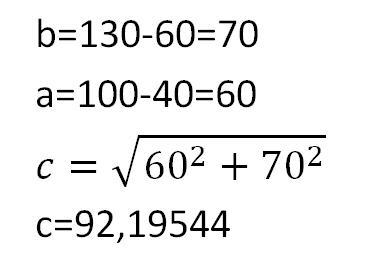
Schritt 2:
Im zweiten Schritt wird bereits der Winkel Alpha 2 berechnet. Hier ist nun jedoch ein schiefwinkliges Dreieck gegeben, weshalb die Berechnung etwas umfangreicher ausfällt.
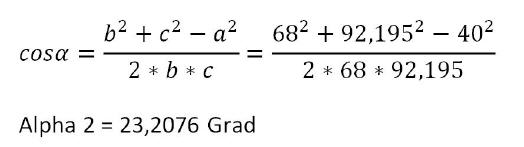
Schritt 3:
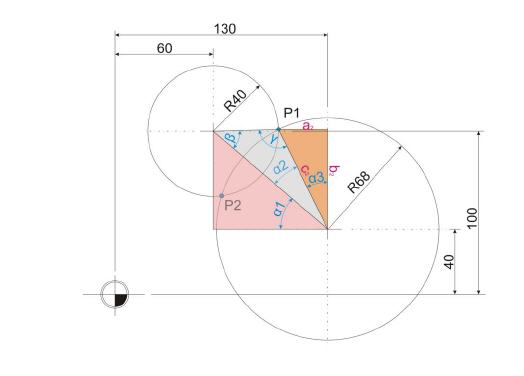
Punkt P1 ist noch nicht bestimmbar, da zwar nun dessen Winkel, doch noch nicht die X- beziehungsweise Y-Entfernung gemessen vom Kreismittelpunkt aus bekannt ist. Diese Werte sollen nun ermittelt werden. Dazu ist zunächst der Winkel Alpha 3 zu ermitteln. Dazu müssen lediglich Summe der beiden nun bekannten Winkeln W1 und W2 von 90 Grad subtrahiert werden.
Alpha 3 = 90 Grad - Alpha 2 – Alpha 1
Alpha 3 = 90 Grad – 40,601Grad – 23,208 Grad
Alpha 3 = 26,191 Grad
Nachdem nun der Winkel dieses Dreiecks bekannt ist, können die beiden Strecken a2 und b2 ermittelt werden.
a2=sin(26,191)*68
a2 = 30,013 Millimeter
b2=cos(26,191)*68
b2=61,018 Millimeter
Punkt P1 könnte nun bereits berechnet werden, doch soll dieser Schritt erst später, gemeinsam mit der Berechnung von Punkt P2 erfolgen.
Schritt 4:
Um Punkt P2 berechnen zu können, muss zunächst der Winkel zwischen Punkt P1 und Punkt P2 ermittelt werden. Dies ist sehr einfach, da dazu nur der Winkel Alpha 2 verdoppelt werden muss.
Alpha 4 = Alpha 2 * 2
Alpha 4 = 23,2076 Grad * 2
Alpha 4 = 46,4152 Grad
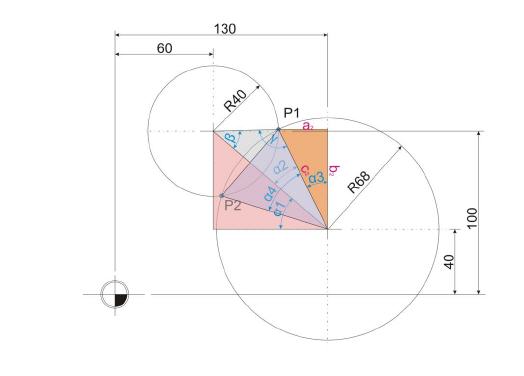
Schritt 5:
Nun werden die Strecken a3 und b3 benötigt, damit die Lage von Punkt P2 bezogen auf den Kreismittelpunkt berechnet werden kann. Zunächst ist dazu die Kenntnis des Winkels Alpha 5 nötig. Dieser wird ebenso einfach wie Alpha 4 ermittelt: Von 90 Grad werden die Winkel Alpha 3 und Alpha 4 abgezogen.
Alpha 5 = 90 Grad – Alpha 3 – Alpha 4
Alpha 5 = 90 Grad – 26,191 – 46,415
Alpha 5 = 17,394 Grad
Nachdem der Winkel bekannt ist,
können die Strecken a3 und b3
ermittelt werden.
a3 = sin(17,394) * 68
a3= 20,328 Millimeter
b3 = cos (17,394) * 68
b3 = 64,891
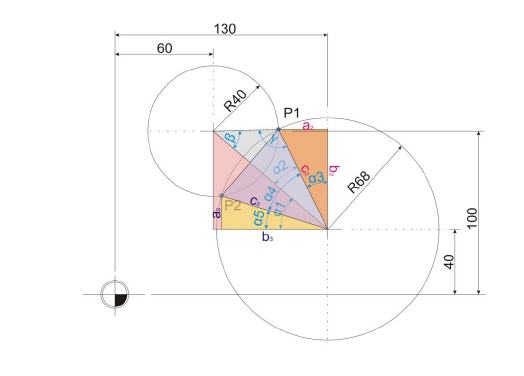
Schritt 6:
Als letzter Schritt können nun die Lagen der Punkte P1 und P2 berechnet werden.
P1 X = 130 – 30,013 = 99,987 Millimeter
P1 Y = 40 + 61,018 = 101,018 Millimeter
P2 X = 130 – 64,891 = 65,109 Millimeter
P2 Y = 40 + 20,328 = 60,328 Millimeter

Download:
Eine Excel-Tabelle zum Berechnen der Schnittpunkte zwischen zwei Kreisen können Sie hier im .XLS-Format [1.296 KB]
herunterladen.
Wichtig: Dieses Excel-Tabelle darf nur als Lehrmaterial verwendet werden. Für wie auch immer geartete Schäden aus ihrer Nutzung wird jede Verantwortung abgelehnt.
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 6 - gesamt: 33723.
















































































