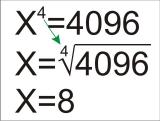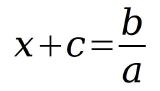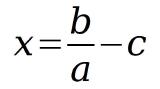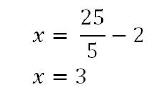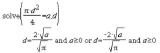Die Grundlagen des Formelumstellens
Mathematik leicht gemacht
Formeln umzustellen ist bis zu einem gewissen Grad keine große Kunst. Schwierig wird es, wenn beispielsweise Klammern aufzulösen sind. Doch auch dies kann nach einem Schema geübt werden. Mit dieser Anleitung gehen künftig viele Formelumstellaktionen wie von selbst, solange die gesuchte Variable nicht mehrmals in der Formel vorkommt.

Natürlich ist jedem in der Schule zu Ohren gekommen, dass es beim Formelumstellen darum geht, dass auf der linken Seite vom Gleichheitszeichen das gleiche Ergebnis herauszukommen hat, wie auf der rechten Seite. Vielfach wird in der Schule zum Verständnis dieses Sachverhalts eine Lebensmittelwaage bemüht, die nur dann im Gleichgewicht ist, wenn beide Schalen das gleiche Gewicht beherbergen.
Dieser Vergleich ist gut gewählt, da dadurch schon einmal grundsätzlich symbolisiert wird, auf was es beim Formelumstellen ankommt: auf der linken und rechten Seite der Formel muss immer das gleiche Ergebnis herauskommen, dann wurde die Formel korrekt umgestellt.
Grundlagen
Für Berechnungen im Bereich der Grundrechenarten ist es recht einfach nachzuvollziehen, wie Formeln umgestellt werden müssen. Wenn man sich das Gleichheitszeichen als „Umwandelzauberzeichen“ denkt, dann wird aus einem Plus-Zeichen beim Hinüberwechseln auf die andere Seite ein Minus-Zeichen und aus einem Minus-Zeichen eben ein Plus-Zeichen. Dies geschieht analog mit den anderen Grundrechenarten: aus „Mal“ wird „geteilt durch“ und aus „geteilt durch“ eben „Mal“. Wichtig: Werden lediglich beide Seiten gegeneinander ausgetauscht, so werden die Vorzeichen nicht verändert!
Das Vorzeichen im Auge behalten
Wichtig ist, dass man sich immer vor Augen hält, dass positive Vorzeichen beim Schreiben der Formel weggelassen werden können. Daher sieht man als beginnender Mathematikexperte nicht sofort, wie man am besten die Umwandlung einer Formel handhaben soll. Deshalb soll man sich zumindest am Anfang angewöhnen, die positiven Vorzeichen manuell nachzutragen:

Vorzeichen beachten!
Dieses Beispiel zeigt den manuellen Nachtrag eines Plus-Zeichens (rote Farbe). Wenn die positive fünf nach rechts wandert, wird aus Plus immer Minus. Das Plus-Zeichen vor dem "X" kann selbstverständlich weggelassen werden. Man sollte sich angewöhnen, stets zunächst die negativen Werte für ein "Hinüberziehen" auszuwählen, um diversen Problemen beim weiteren Auflösen der Formel schon im Vorfeld aus dem Weg zu gehen, wie das nächste Beispiel mahnt.
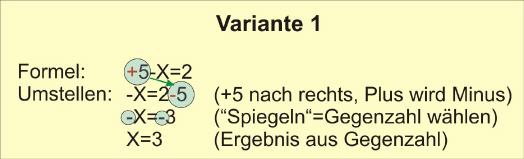
Wie Variante 1 zeigt, ist das Ergebnis ein negativer Wert, der sich darüber hinaus auf ein negatives "X" bezieht.
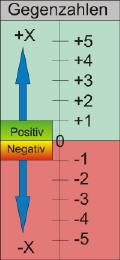
Hier müssen nun Gegenzahlen ins Spiel kommen, um das korrekte Ergebnis mit einem positiven „X“ zu erhalten. Gegenzahlen sind nichts anderes, als gespiegelte Werte. Man kann sie auch mit Materie und Antimaterie vergleichen, die sich lediglich in ihrem Vorzeichen (der Ladung) unterscheiden. Ähnlich einem Thermometer gibt es einen positiven und einen negativen Bereich, auf dem die jeweilige Gegenzahl eines Wertes diesem genau spiegelbildlich gegenüberliegt.
Will man vermeiden, beim Formelumstellen mit Gegenzahlen in Berührung zu kommen, sollte stets versucht werden, zunächst alle negativen Werte durch Ziehen auf die „andere Seite“ in positive Werte umzuformen. Dies zeigt Variante 2. Hier steht am Ende der Formelumstellung ein positives „X“ mit dem korrekten Ergebnis.
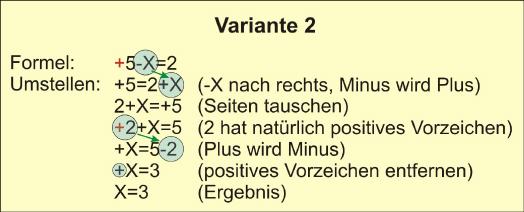
Punkt vor Strich-Regel beachten
Aus einer Multiplikation wird beim hinüberziehen eine Division. Beim Formelumstellen gilt übrigens auch das Punkt vor Strich-Gesetz, sodass niemals versucht werden sollte, zunächst etwa die positive fünf nach rechts zu ziehen.

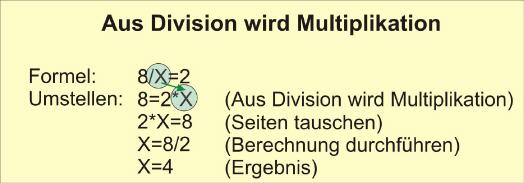
Analog muss im Fall einer Division vorgegangen werden. Nach dem Seitentausch wird daraus eine Multiplikation. Sollte nun das X-Zeichen rechts stehen, so können beide Seiten komplett getauscht werden, was den weiteren Rechengang erleichtert.
Wurzeln und Potenzen
Wurzeln sind das Gegenstück zu Potenzen und umgekehrt. Logisch, dass sich beide beim Seitentausch in das jeweilige Gegenstück verwandeln. Wenn der Potenzwert größer ist als 2, dann wird bei Seitentausch eine entsprechend wertige Wurzel, um die Waage im Gleichgewicht zu halten. Aus der 4. Potenz wird daher immer die 4. Wurzel.
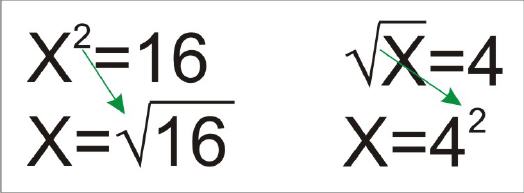
Klammern auflösen
Klammern haben eine Gruppenfunktion. Sie fassen Rechenfunktionen zusammen und geben diesen eine neue Gewichtung. Beispielsweise kann mit Klammern die Punkt-vor-Strich-Regel aufgehoben werden.
In diesem Beispiel werden zunächst die beiden Werte von x und c addiert und der daraus entstandene Wert mit a multipliziert. Wenn nun der Wert x unbekannt ist, die anderen Werte jedoch bekannt sind, dann muss die Formel lediglich nach x umgestellt werden.
Wie bereits bekannt, muss zunächst die Variable a auf die andere Seite. Die Klammer kann nun verschwinden, da die Variablen x und c nun alleine stehen und deren Rechenvorrecht von keiner anderen Variablen gestört werden kann.
Zuletzt wird nun die Variable c auf die andere Seite gebracht. Aus Plus wird ja bekanntlich Minus, wenn eine positive Zahl oder eine Variable mit positivem Vorzeichen auf die Gegenseite kommt.
Wenn nun die Variablen mit Werte versehen werden, kann geprüft werden, ob die Umstellung gelungen ist.
Hinweis:
Ein Bruchstrich bedeutet immer, dass hier eine Division stattfindet. Daher sind Bruch und Divisionszeichen gleichwertig. Die Formel hätte also auch wie nebenstehend geschrieben werden können.
Wichtige Merkregeln zum Auflösen von Klammern

Klammerregel 1

Klammern dürfen einfach aufgelöst werden, wenn ein Plus-Zeichen davor steht. Steht ein Minus-Zeichen vor der Klammer, müssen die Zeichen innerhalb der Klammer jeweils umgekehrt werden.
Klammerregel 2

Steht vor der Klammer ein Multiplikator-Zeichen, so müssen zum Auflösen der Klammer die in der Klammer stehenden Glieder mit dem Multiplikator malgenommen werden.
Klammerregel 3

Steht vor der Klammer ein Multiplikator-Zeichen, so müssen zum Auflösen der Klammer die in der Klammer stehenden Glieder mit dem Multiplikator malgenommen werden.Hinweis: obiger Ausdruck wird in der Regel ohne Mal-Zeichen geschrieben: ab+ac. Zum besseren Verständnis wird hier jedoch darauf verzichtet, um den Lernerfolg nicht zu gefährden.
Wichtig:
Um beim Auflösen der Klammer durch eine Multiplikation das korrekte Ergebnis zu erhalten, muss immer das Vorzeichen vor der Zahl oder der Variablen beachtet werden!
+a*(b-c)=a*b-a*c
Erklärung:
+a*+b=+ab
+a*-c=-ac
Ergebnis: +ab-ac
Positive Vorzeichen werden nicht geschrieben, daher gilt folgendes Endergebnis: ab-ac
Klammerregel 4
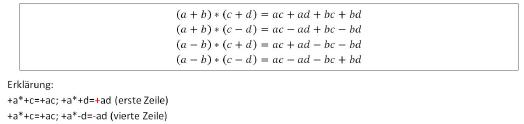
Zwei Klammern können aufgelöst werden, wenn die Klammerglieder in den beiden Klammern miteinander multipliziert werden.
Entscheidend ist also immer das Vorzeichen des Ergebnisses der Multiplikation. (Siehe Merkregeln zum Auflösen von Klammern: Minus mal Minus ergibt Plus etc.)
Klammerregel 5
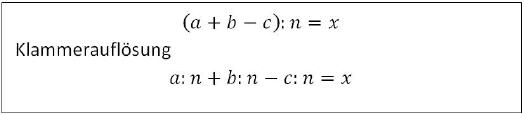
Wenn Klammerausrücke durch einen Wert dividiert werden müssen, dann kann die Klammer aufgelöst werden, indem jedes Glied der Klammer durch diesen Wert dividiert wird.
Klammerregel 6
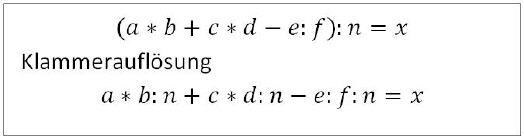
Werden in der Klammer Multiplikationen vorgenommen, so wird das Ergebnis jeweils mit dem Divisor dividiert. Dies auch dann, wenn in der Klammer Divisionen vorkommen.
Klammerregel 7
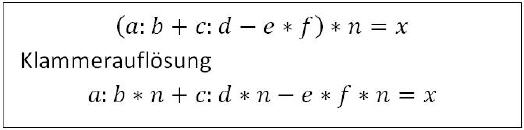
Werden Ausdrücke in der Klammer multipliziert, so ergibt sich das gleiche Bild.
Klammerregel 8
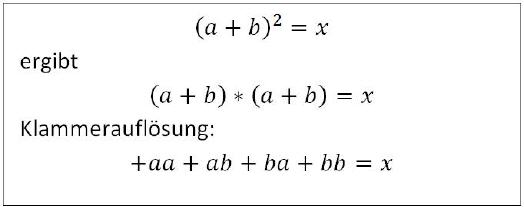
Die Merkregeln bezüglich der Vorzeichen müssen stets beachtet werden, um Klammern erfolgreich aufzulösen.
Klammerregel 9
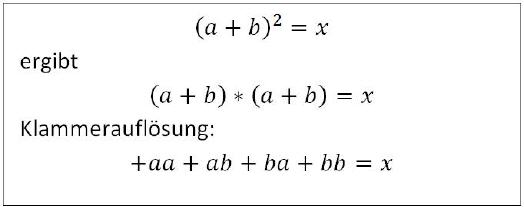
Die Merkregeln bezüglich der Vorzeichen müssen stets beachtet werden, um Klammern erfolgreich aufzulösen.
Merke:
Klammern müssen stets von innen nach außen aufgelöst werden.
Beispiele zum Thema Formelumstellen

Formelumstellen mit CAS-Produkten
Seit geraumer Zeit gibt es Programme und Taschenrechner, mit denen Formeln nach beliebigen Buchstaben aufgelöst werden können. Beispielhaft sollen diese Möglichkeit mit der PC-Software „Mathcad“ und der nspire-Taschenrechnerserie von Texas Instruments vorgestellt werden. Wichtig: egal, welcher Hersteller gewählt wird, stets muss der Taschenrechner oder das PC-Programm mit CAS ausgestattet sein, da sonst die Formelumstellmöglichkeit nicht gegeben ist.
Mathcad
Mathcad gibt es mittlerweile in der Version 15 und ist für Schüler und Studenten sehr preiswert beziehbar. Vor geraumer Zeit gab es die Version 8 gar als Zugabe auf diversen Computerzeitschriften-CDs. Wer damals Zugriff, hatte einen Software-Rechenboliden für wenig Geld ergattert, der auch heute noch gute Dienste tut.
Mathcad arbeitet ähnlich, wie moderne Taschenrechner. Das heißt, man kann eine Formel direkt so eingeben, wie man sie auch auf das Papier schreiben würde. Mit ein wenig Übung geht die Formeleingabe leicht von der Hand. Für die Eingabe der Flächenformel wird folgende Vorgehensweise empfohlen:
Zunächst wird per linken Mausklick der rote Cursor an eine beliebige Stelle der Eingabefläche Platziert. Danach gibt man per Tastatur den Buchstaben A ein, gefolgt von einem Mausklick auf das Zeichen „Bolescher Operator“ im Menu „Auswertung“. Danach das Divisions-Zeichen per Tastatur oder per Klick auf den entsprechenden Button im Menü „Arithmetisch“ eingeben. Dadurch wird die Möglichkeit geschaffen, die Formel nach Vorgabe einzugeben. Das griechische Zeichen Pi (π) wird über den entsprechenden Button im Menü „Griechisch“ erzeugt. Ein Hochzeichen über den Buchstaben „d“ erhält man, indem der Button „Quadrieren“ im Menü „Arithmetisch“ betätigt wird. Die Eingabe der Zahl 4 ist mit den Cursor-Tasten ein wenig knifflig, da man sehr schnell die Formel verlässt und auf dem Eingabefeld landet. Sicherer ist es daher, den Platzhalter, an dem die Zahl 4 eingegeben werden soll, mit der Maus auszuwählen.
Wenn nun diese Formel nach einem bestimmten Buchstaben umgestellt werden soll, genügt es, den Button „auflösen“ zu betätigen. Mathcad ergänzt nun die Formel mit dem Text „auflösen“, gefolgt von einem Platzhalter. Hier kann der gewünschte Buchstabe eingegeben werden, nach dem die Formel aufgelöst werden soll. Nachdem hier der Buchstabe „d“ eingegeben wurde, genügt ein Druck auf die Taste „Return“, um den Umstellvorgang auszulösen. Mathcad präsentiert hier zwei Lösungen, die beide zum gewünschten Ergebnis führen. Allerdings ist festzustellen, dass die eigenhändig umgestellte Formel eleganter, da leichter nachvollziehbar, ist.
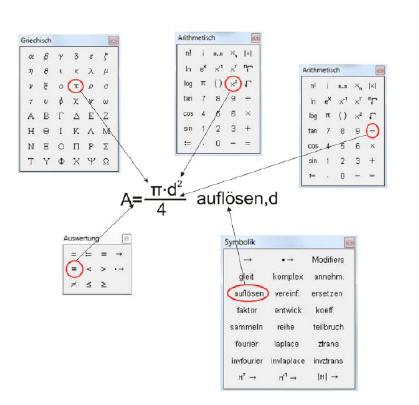
Formelumstellen per Mathcad
Um eine Formel von Mathcad umstellen zu lassen, muss das Zeichen "Boolescher Operator" in der Palette "Auswertung" verwendet werden.
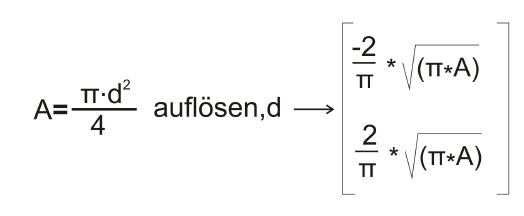
Matcad präsentiert zwei Ergebnisse, die beide zum gewünschten Ergebnis führen.
TI-Nspire cx CAS
Trotz des Aufkommens der kompakten Netbooks, auf denen neben Mathcad noch andere Software läuft, haben Taschenrechner, wie die Nspire cx CAS-Serie von Texas Instruments ihren treuen Freundeskreis. Und das zu Recht, ist in diesen Produkten pure Rechenkraft noch einmal ein Stück kompakter verpackt und die Betriebsdauer der Akkus entscheidend länger. Leider weicht die Handhabung dieser Rechenboliden ganz gehörig von der Bedienung herkömmlicher Taschenrechner ab. Viele Funktionen sind nicht direkt per Tastatur erreichbar, sondern verstecken sich in diversen Menüs, was eine intensive Einarbeitung nötig macht, um den mächtigen Rechenumfang voll auszuschöpfen. Die Flächenformel wird hier auf folgende Weise eingegeben und umgestellt:
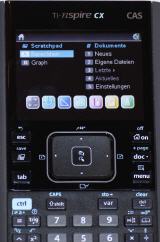
Nach dem Einschalten des Rechners erscheint ein Auswahlbildschirm. Dieser kann mit den Cursortasten, die im sogenannten „Touchpad“ des Rechners integriert sind, durchwandert werden, wodurch verschiedene Funktionen angewählt werden können. Zur Formelumstellung wird das sogenannte „Scratchpad“ benötig, das sich hinter dem Auswahlmenü „A Berechnen“ verbirgt. Nachdem „A Berechnen“ angewählt wird, kann durch Drücken der mittleren Fläche des Touchpad diese Auswahl bestätigt werden, woraufhin das Scratchpad erscheint. Hier können nun alle Berechnungen wie mit herkömmlichen Taschenrechnern durchgeführt werden.

Touchpad des TI Nspire-Rechners
Zum Umstellen von Formeln wird die Funktion „Solve“ benötigt. Diese findet sich in einem Menü, das man über die gleichlautende Taste erreicht. Nachdem die Taste gedrückt wurde und das Menü sichtbar ist, wird der Cursor zur Auswahl „3 Algebra“ gesetzt und mit der Cursortaste „rechts“ ein weiteres Menü aufgerufen. Gleich der erste Eintrag lautet „Löse“. Hinter dieser Bezeichnung verbirgt sich die Solve-Funktion. Ein Druck auf die Mitte der Touchpadfläche bewirkt, dass diese aufgerufen wird.
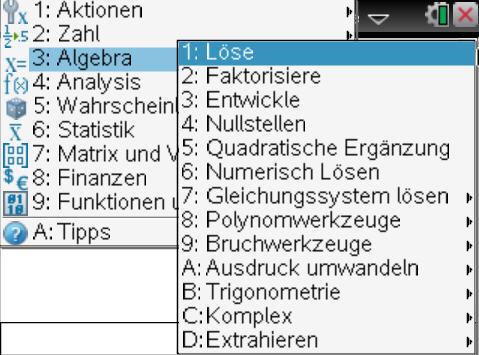
Die Eingabe einer Formel erfolgt nun über wenige Tasten, die wiederum teilweise Menus aufrufen, hinter denen sich weitere Funktionen befinden, die sich auf herkömmlichen Taschenrechnern in der zweiten oder dritten Ebene befinden, wenn sie überhaupt implementiert sind, denn die Nspire-Rechner von Texas Instruments besitzen eine Rechenkraft, die sich gewaschen hat.
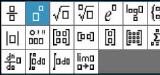
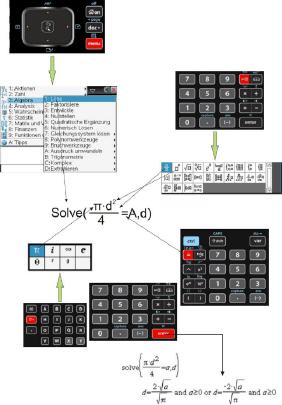
Um einen Bruch einzugeben, muss zunächst die Formel-Taste betätigt werden. Per Cursor wird der erste Eintrag ganz links oben ausgewählt. Der Eintrag „Solve“ ist nun zwischen den Klammern mit einem Bruchzeichen und zwei Platzhaltern gefüllt worden. Oben wird das Pi-Zeichen eingefügt, was über die Taste „Sonderzeichen“ erfolgt. Zufällig hat diese Taste das Pi-Zeichen aufgedruckt. Nachdem diese Taste gedrückt wurde, erscheint ein Auswahlfeld, aus dem man das gewünschte Zeichen wählen kann. Pi steht links oben und wird per Druck auf die Touchpadfläche übernommen.
Die Grundrechenarten haben eigene Tasten und müssen nicht erst aus einem Menü ausgewählt werden. Das Multiplikator-Zeichen nach Pi kann daher rasch eingegeben werden. Zur Eingabe von d2 wird natürlich wieder die Formel-Taste benötigt. Diesmal wird die zweite Funktion links oben ausgewählt. Die Eingabe des Buchstaben „d“ erfolgt über die „Schreibmaschinentastatur“. Danach wird der Cursor in den Platzhalter für die Zahl 2 verschoben und diese Zahl per Druck auf die Zwei aus dem Zahlenblock eingefügt.
Der Cursor wird nun nach unten in den letzten Platzhalter bewegt und aus dem Zahlenblock die 4 betätigt. Nun muss das Gleichheitszeichen „=“ erzeugt werden. Dazu wird der Cursor nach rechts bewegt und diese Zeichen mit der entsprechenden Taste ohne Umweg über ein Menü eingefügt. Um zum Schluss nun den Buchstaben A als Flächenzeichen einzugeben, genügt es, auf Großschreibung per Shift-Taste umzuschalten und die Taste A zu betätigen.
Die Formel wäre nun komplett eingegeben. Um den Rechner nun zu veranlassen, diese nach „d“ aufzulösen, muss lediglich an die Formel der gewünschte Buchstabe hinzugefügt werden. Natürlich muss dieser Buchstabe, nach der die Formel umgestellt werden soll, durch ein Komma von der Formel getrennt werden, damit dies klappt. Das Komma hat eine eigene Taste und der Buchstabe wird wie gehabt über die „Schreimaschinentastatur“ eingegeben.
Nachdem die Taste „enter“ gedrückt wurde, wird die Formel umgestellt. In diesem Fall sind zwei Lösungen möglich, die beide zum korrekten Ergebnis führen. Wie zu sehen ist, gibt der Rechner eine andere Lösung aus, wie Mathcad. Und die „zu Fuß“ umgestellte Formel sieht wieder völlig anders aus. Hier bekommt der Spruch, dass viele Wege nach Rom führen, eine weitere Bestätigung.
Download
Diesen Artikel können Sie hier im PDF-Format [2.221 KB]
herunterladen.
Ein PDF-Skript zum Umgang mit Mathcad finden Sie hier [680 KB]
.
Ein PDF-Skript zum Umgang mit dem TI Nspire CAS gibt es hier [990 KB]
.
Video
Videos zum Umstellen von Formeln und Auflösen von Klammern finden Sie zahlreich:
Video 1: Formeln mit Mathcad umstellen
Video 2: Formeln mit TI Nspire umstellen
Animationsvideos:
Video 3: Aus Minus wird Plus
Video 4: Aus Plus wird Minus
Video 5: Winkelfunktion
Video 6: Flächenberechnung
Video 7: Volumenberechnung
Video 8: Klammern auflösen Teil 1
Video 9: Klammern auflösen Teil 2
Video 10: Klammern auflösen Teil 3
Video 11: Klammern auflösen Teil 4
Video 12: Klammern auflösen Teil 5
Video 13: Klammern auflösen Teil 6
Video 14: Klammern setzen
Video 15: Potenz umwandeln
Video 16: Wurzel umwandeln
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 4 - gesamt: 19513.