Optimale Bestellmenge berechnen
Die Lagerkosten im Griff
In der Serienfertigung ist vorab bekannt, wie hoch die Stückzahl des hergestellten Produkts pro Jahr zu sein hat. Entsprechend muss dafür gesorgt werden, dass im Lager immer ausreichend Material vorhanden ist, um das Produkt reibungslos fertigen zu können. Dabei kommt es darauf an, nicht zu viel und nicht zu wenig Material zu lagern, da im ersten Fall die Lagerkosten unnötig hoch werden und im anderen Fall die Produktion gefährdet ist. Für solche Fälle gibt es schlaue Formeln.
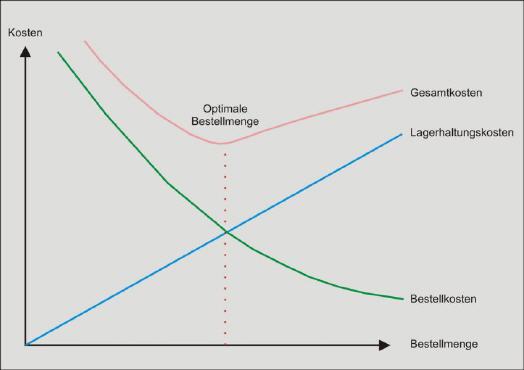
Die Tätigkeit in einem Lager ist alles andere als Trivial. Die dort beschäftigten Verantwortlichen müssen dafür sorgen, dass der in der Produktion erzielte Mehrwert durch das Veredeln von Halbzeugen nicht durch übermäßig hohe Lagerkosten mehr als unvermeidbar geschmälert wird. Es gilt, den Bestellvorgang so genau zu planen, dass dieser in regelmäßigen Abständen erfolgt, bei dem eine genau berechnete Stückzahl neuer Ware erworben wird. Der Grund: Die Höhe der Bestellung hat sowohl Einfluss auf die Bestell- als auch auf die Lagerhaltungskosten.
Hier kommt daher die sogenannte ›Bestellmengenrechnung‹ zum Einsatz, um die optimale Bestellmenge zu ermitteln. Hier geht es darum, zu ermitteln, wann die Summe der Beschaffungs- und Lagerkosten bezogen auf die Beschaffungsmenge am geringsten ist.
Diese Bestellmengenrechnung muss jedoch mit Einschränkungen leben und dient nur der Annäherung an die Realität. Der Grund liegt darin, dass man von Annahmen ausgeht, die unter Umständen in der Realität nicht immer zutreffen. Zum Beispiel muss der Bedarf über einen längeren Zeitraum konstant sein und die Entnahmen aus dem Lager sollten kontinuierlich erfolgen. Zudem geht man davon aus, dass die Lagerkosten konstant sind und die Liquidität zur Beschaffung des benötigten Materials vorhanden ist. Darüber hinaus wird davon ausgegangen, dass der durchschnittliche Lagerbestand der halben Bestellmenge entspricht.
Werden Waren verwendet, die an den Weltmarktpreis gekoppelt sind, wie etwa Zinn, Zink oder Silber, so kann es aus Kostensicht wesentlich effizienter sein, solche Waren sofort zu beschaffen, wenn sich eine Phase steigender Preise ankündigt. Das Einhalten einer optimalen Bestellmenge ist dann zwar nicht mehr möglich, dennoch kann sich im Endeffekt dieses Vorgehen durch weiter steigende Preise lohnen.
Formel nach Andler:

Bei obiger Formel wird noch nicht ein eingeräumter Rabatt berücksichtigt, den man bei Abnahme einer bestimmten Menge bekommt. Mit der Formel von Erich Kosiol ist auch dies zu berücksichtigen.
Formeln nach Kosiol:

Diese Formel ist etwas genauer, als die von Andler. Wer konsequent die optimale Bestellmenge berechnet, wird mit einer wesentlichen Senkung der Lagerbestände sowie einem beträchtlichen Rückgang der Bestellungen von Kleinmaterial belohnt.
Doch gibt es natürlich zu beachten, dass die optimale Bestellmenge durchaus so groß sein kann, dass entweder der Lieferant diese Menge nicht liefern kann oder das eigene Lager diese Menge gar nicht aufnehmen kann. In diesem Fall muss vorab entsprechend das Problem geklärt werden.
Optimale Bestellhäufigkeit:
Auch die Anzahl der Bestellungen wirkt sich auf die Wirtschaftlichkeit eines Lagers aus. Selbstverständlich gibt es auch dafür eine passende Formel, um diesen Wert zu ermitteln:
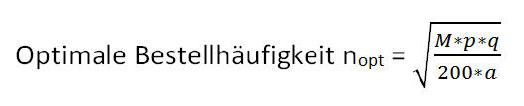
Hinweis: Die Variablen entsprechen denjenigen der optimalen Bestellmenge.
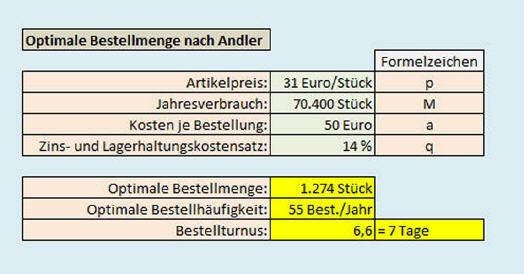
Beispiel optimale Bestellmenge:
| Gegeben: | Jahresverbrauch: | 70.400 Stück |
| Kosten je Bestellung: | 50 Euro | |
| Artikelpreis: | 31 Euro/Stück | |
| Zins- und Lagerhaltungskostensatz: | 14 Prozent |
Berechnung optimale Bestellmenge:
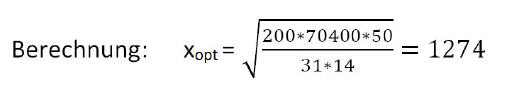
Die optimale Bestellmenge beträgt 1.274 Stück.
Berechnung optimale Bestellhäufigkeit:
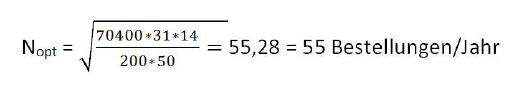
Es müssen 55 Bestellungen pro Jahr getätigt werden.
Berechnung Bestellturnus:
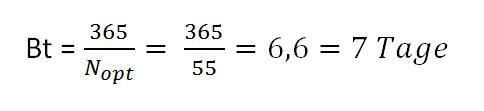
Alle 7 Tage müssen 1274 Stück des Artikels bestellt werden.
Probe zur Kontrolle:
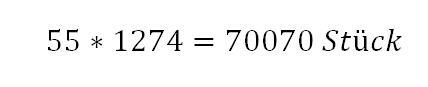
Fehler: 70400-70070 = 330 Stück
Der deutlich unter der optimalen Bestellmenge liegende Fehler (bezogen auf die benötigte Jahresmenge) zeigt, dass die Berechnung korrekt erfolgte.
Download:
Eine Excel-Tabelle zum Berechnen der optimalen Bestellmenge finden Sie hier [33 KB] .
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 3 - gesamt: 4320.















































































