Berührpunktberechnung Kreis-Tangente
Dreiecksberechnung ohne Mühe
Die Dreiecksberechnung ist ein Tausendsassa in der Geometrie. Es gibt nahezu kein Geometrieproblem, das damit nicht gelöst werden kann. Wenn eine Gerade einen Kreis berührt, spricht man von einer Tangente. Die Ermittlung des Berührpunkts ist mit der richtigen Rechentechnik rasch erledigt.
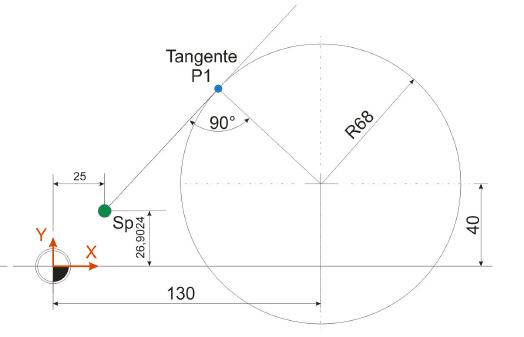
Wie bereits beim vorhergehenden Kurs angesprochen, gilt auch diesmal folgender Rat: Bevor dieses Manuskript durchgearbeitet wird, empfiehlt sich die Lektüre des Skripts ›Berechnung der Schnittpunkte zwischen zwei Kreisen‹. Erst mit dieser Grundlage kann an dieser Stelle sinnvoll weitergelesen werden, da sonst wesentliche Dinge unbekannt bleiben.
Folgende Beschreibung erhebt keinen Anspruch, den besten Rechenweg zur Berechnung einer Tangente zu beschreiben. Wie hinreichend bekannt, führen immer mehrere Wege ans Ziel. Nicht alle Wege sind jedoch für jeden gleichermaßen geeignet. Der vorgeschlagene Lösungsweg zum Berechnen einer Tangente, die sich beim Berühren einer Geraden an einem Punkt eines Kreise ergibt, ist daher nicht unbedingt jedermanns Favorit. Er kommt jedoch den Fachleuten entgegen, die gerne die Dreiecksberechnung zur Lösung geometrischer Aufgaben heranziehen.
Schritt 1:
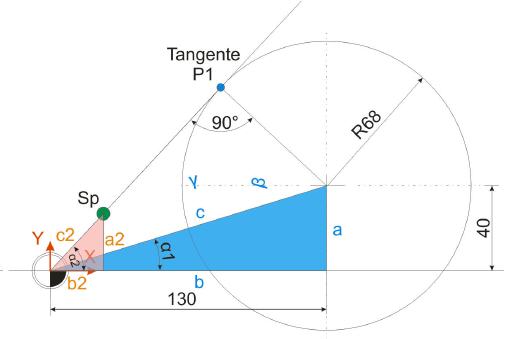
Im ersten Schritt der Berechnung des Berührpunktes ist es nötig, die Strecke c der Hypotenuse des blauen Dreiecks zu ermitteln. Die Ankathete a (40 mm) sowie die Gegenkathete b (130 mm) sind bekannt und werden für diese Berechnungen herangezogen.
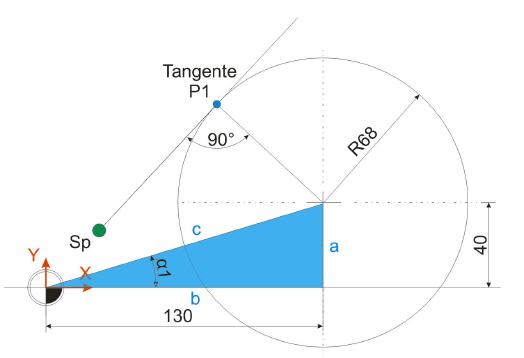
Die Länge der Strecke c, also der Geraden zwischen dem Nullpunkt und dem Kreismittelpunkt, ist wie folgt zu ermittel:
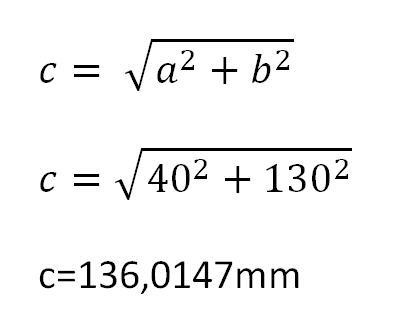
Zusätzlich ist noch der Winkel Alpha 1 zu ermitteln.
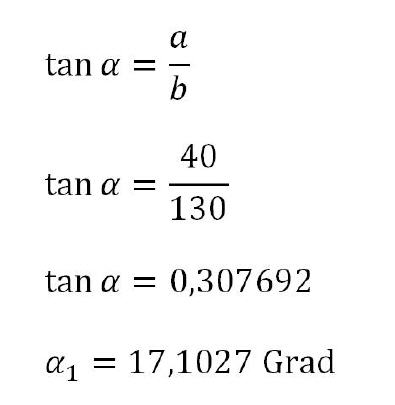
Schritt 2:
Im nächsten Schritt wird der Winkel Alpha 2 ermittelt, da dieser nötig ist, um im späteren schiefwinkligen Dreieck alle benötigten Werte für die Berührpunktberechnung zu besitzen.
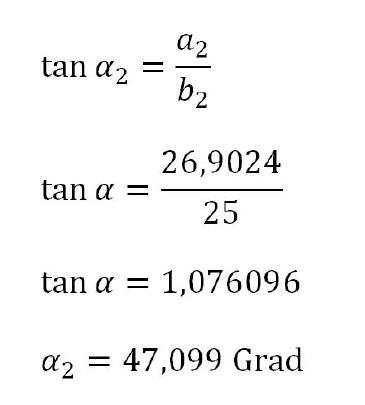
Schritt 3:
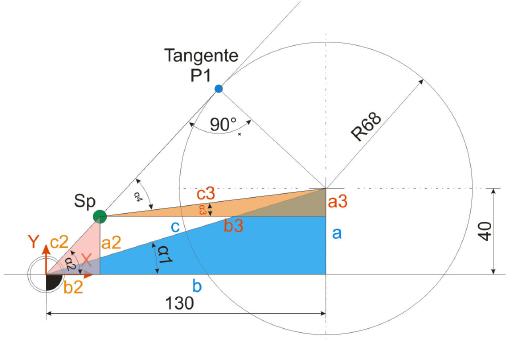
Für den nächsten Schritt werden die Werte die Strecke c3 sowie der Winkel Alpha 3 und Alpha 4 berechnet. Die Werte a3 und b3 sind unschwer ermittelt, da sich diese aus bereits bekannten Punkten errechnen lassen.
b3 = 130-b2 = 130-25 = 105 mm
a3 = 40-a2 = 40-26,9024 = 13,0976 mm
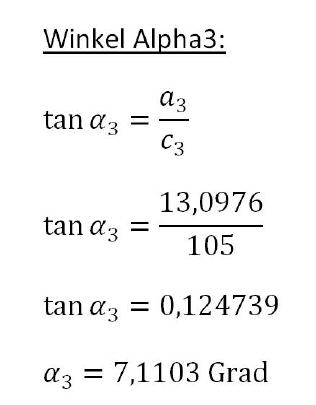
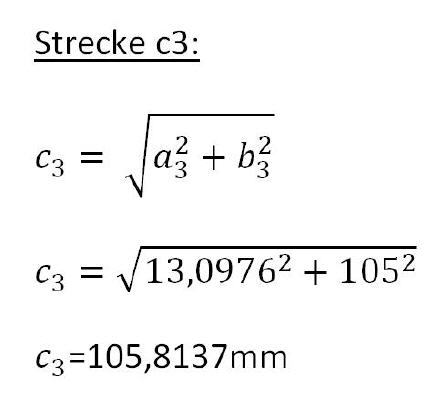
Winkel Alpha 4 = Winkel Alpha 2 - Winkel Alpha 3 = 47,099-7,1103
Winkel Alpha 4 = 39,989 Grad
Schritt 4:
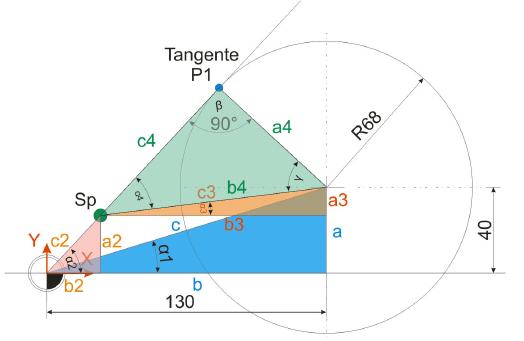
In Schritt 4 muss ein schiefwinkliges Dreieck bemüht werden, um die Strecke c4 zu ermitteln, da diese der Schlüssel zum Berechnen des Berührpunktes P1 ist. Doch zunächst muss der Winkel Gamma berechnet werden. Dazu ist die Erkenntnis heranzuziehen, dass die Summer aller Winkel im Dreieck stets 180 Grad beträgt. Nachdem die Winkel Beta und Alpha 4 bekannt sind, kann mit diesem Wissen der fehlende Winkel Gamma berechnet werden.
Winkel Gamma = 180-(Winkel Beta + Winkel Alpha 4) = 180-(90+39,989)
Winkel Gamma = 50,011 Grad
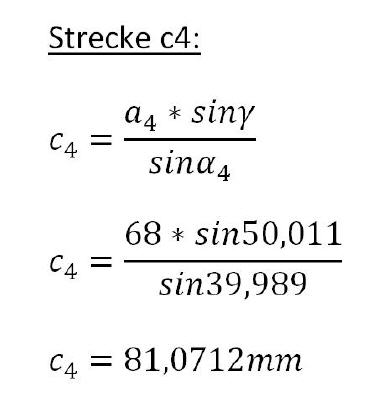
Schritt 5:
In Schritt 5 kann nun die Lage des Berührpunktes bestimmt werden. Dazu werden lediglich noch der Winkel Alpha 5 sowie die Strecken a5 und b5 benötigt.
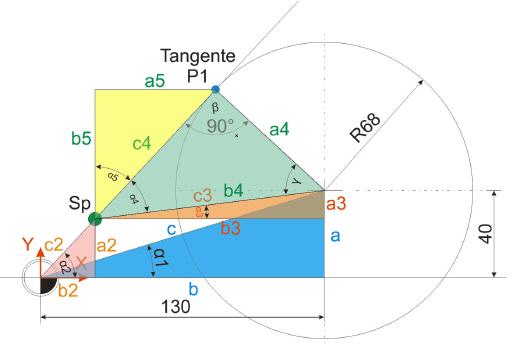
Winkel Alpha 5 = 90-(Winkel Alpha 4 + Winkel Alpha 3) = 90-(36,989+7,1103)
Winkel Alpha 5 = 42,9007 Grad


Schritt 6:
Mit den ermittelten Werte kann nun der Berührpunkt errechnet werden.
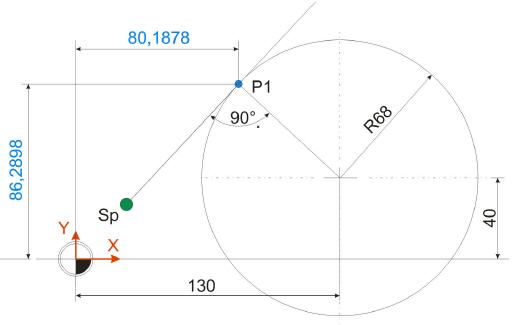
P1(X) = b2+a5 = 25+55,18758 = 80,1876 mm
P1(Y) = a2+b5 = 26,9024+59,3875 = 86,2899 mm
Download:
Eine Excel-Tabelle zum Berechnen des Berührpunkts Kreis-Tangente können Sie hier im XLS-Format [683 KB] herunterladen.
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 7 - gesamt: 17954.
















































































