Ein Hochleistungsakku im Miniformat
Kondensatoren als Energiesammler
Kondensatoren sind wichtige Elektronikbauteile, ohne die elektronische Schaltungen nicht funktionieren würden. Der Grund: Sie haben die Eigenschaft, Strom rasch aufzunehmen und wieder abzugeben. Dadurch sind sie in der Lage, kurzzeitige Stromschwankungen auszugleichen. Zeit, mehr über diese wichtigen Bauteile zu erfahren.

Was würde wohl ein Gärtner sagen, wenn aus seinem Wasserschlauch keine konstante Wassermenge, sondern ein an- und abschwellender Wasserstrom fließen würde? Er würde dem Wasserwerk sicher mitteilen, dass diese gefälligst einen Wasserspeicher installieren sollen, damit der Wasserdruck in der Leitung konstant bleibt und er seine Pflanzen anständig gießen kann.
In unseren Stromleitungen ist genau dieses für den Gärtner ärgerliche Phänomen zugegen: ein ständig an- und abschwellender Strom von Elektronen. Mit einer Frequenz von 50 Herz erreicht in Deutschland der Wechselstrom die Haushalte. Dies bedeutet, dass 50 Mal pro Sekunde in den Stromleitungen die Spannung rauf- und runtergeregelt wird, wobei beim Mittelwert überhaupt kein Strom fließt.
Kurzzeitiges Ausbleiben von Strom muss ausgeglichen werden, sollen elektrische Schaltungen zuverlässig funktionieren. Hier kommen sogenannte ›Kondensatoren‹ ins Spiel. Diese haben die Eigenschaft, eine geringe Menge Strom physikalisch in kurzer Zeit aufzunehmen und rasch wieder abzugeben. Sie haben die Aufgabe, Stromlücken zu überbrücken. Dies ist ihnen möglich, da sie praktisch wie ein extrem leistungsfähiger Akku arbeiten, ohne jedoch dessen hohe Stromspeichereigenschaft zu besitzen. Allerdings können sie im Gegensatz zu Akkus ohne Leistungsverlust beliebig oft ge- und entladen werden. Es gibt sie in verschiedensten Bauformen und Größen, wobei die Größe bereits einen Rückschluss auf Ihre Stromaufnahmefähigkeit gibt.
Eine enorme Bedeutung haben Kondensatoren in Computer-Speicherbausteinen (DRAM), wo sie für das Speichern von Information zuständig sind.

Arbeitsweise von Kodensatoren:
Kondensatoren besitzen prinzipiell alle den gleichen Aufbau in Form von zwei Platten, die sich gegenüberstehen und von einem isolierenden Medium getrennt werden. Mit dem Abstand der Platten ist die Kapazität eng verbunden: Wird der Abstand um die Hälfte des Ausgangsabstands verringert, so steigt die Kapazität auf den doppelten Ursprungswert.
Wird nun eine Gleichspannung am Kondensator angeschlossen, so werden dessen Elektroden aufgeladen und eine Spannung aufgebaut. Wird die Stromquelle abgeschaltet, so bleibt die Ladung des Kondensators erhalten. Sobald ein Verbraucher am Kondensator zwischengeschaltet wird, fließt dessen Ladung ab und bewirkt eine Arbeitsleistung im Verbraucher, was beispielsweise durch kurzes Aufleuchten einer Lampe sichtbar wird.
Wie viel Strom speichern Kondensatoren?
Kondensatoren können nur vergleichsweise geringe Strommengen speichern. Die Kapazität wird in der Einheit Farad (F) angegeben. In der Regel besitzen gängige Kondensatoren jedoch nur einen Bruchteil eines Farads. Gängige Angaben sind das Mikrofarad (µF), das Nanofarad (nF) und das Picofarad (pF).
Hier gilt folgende Beziehung:
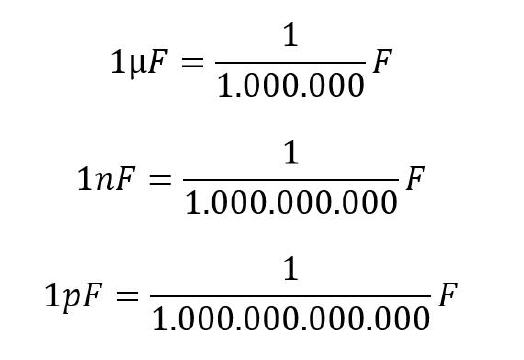
Zahlenwerte auf Kondensatoren einordnen
Leider werden Kondensatoren nicht einheitlich gekennzeichnet. Oft ist die Kapazität codiert aufgedruckt. So wird beispielsweise mit der Angabe 103 in den ersten beiden Stellen der Kapazitätsbasiswert angegeben, während die letzte Zahl die Zehnerpotenz repräsentiert. Das Ergebnis ist die Kapazität in Picofarad. Somit hat der Kondensator mit dem Aufdruck ›103‹ eine Kapazität von 10.000 pF, was umgerechnet 10 nF entspricht. Die Angabe 471 bedeutet daher entsprechend eine Kapazität von 470 pF, während die Angabe 101 einer Kapazität von 100 pF und die Angabe 106 einer Kapazität von 10.000.000 pF entspricht.
Manchmal wird dem Zahlenwert ein Kleinbuchstabe vorangestellt, wodurch das Umrechnen entfällt. Die Bezeichnung n47 beispielsweise bedeutet eine Kapazität von 0,47 nF.
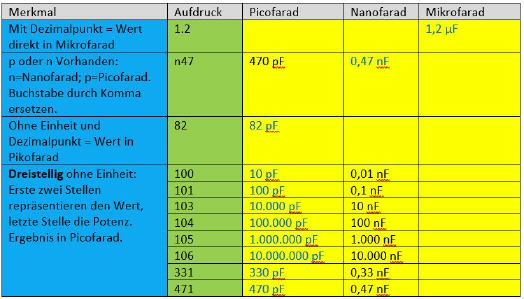
Nachfolgendes Bild zeigt Kondensatoren mit dem Aufdruck 101. Diese Kondensatoren haben demnach eine Kapazität von 100 pF, da die ersten beiden Zahlen (10) den Kapazitätsbasiswert ergeben, dem noch eine Null (1) angehängt wird. Das Ergebnis der Berechnung ist die Kapazität des Kondensators.

Allerdings sind die oft sehr klein aufgedruckten Kapazitätsangaben mit dem freien Auge teils gar nicht mehr zu lesen. Aus diesem Grund lohnt sich die Anschaffung einer stark vergrößernden Lupe. Nachfolgendes Bild zeigt zwei Kondensatoren, deren Kapazität ohne Lupe nur schwer lesbar ist.

Durch den Einsatz einer Lupe kann festgestellt werden, dass der linke Kondensator mit ›n47‹ und der recht mit ›1.2‹ bezeichnet ist. Demnach handelt es sich laut obiger Merkmaltabelle um Kondensatoren mit 0,47 nF beziehungsweise mit 1,2 µF Kapazität.
Der Elektrolytkondensator:
Elektrolytkondensatoren besitzen eine vergleichsweise große Stromspeicherkapazität, weshalb sie gerne als Stützkondensatoren in Spannungsversorgungen verwendet werden. Von Nachteil ist, dass Elektrolytkondensatoren mit einer Flüssigkeit gefüllt sind, die als Elektrolyt arbeitet. Diese Flüssigkeit verflüchtigt sich, weshalb Elektrolytkondensatoren im Laufe der Zeit (einige Jahrzehnte) austrocknen oder auslaufen, daher das damit bestückte Elektrogerät irgendwann die Funktion einstellt. Es sollte also im Fall eines defekten Geräts bei der Fehlersuche zunächst die Ursache bei den verbauten Kondensatoren gesucht werden.
Elektrolytkondensatoren dürfen nur mit Gleichspannung betrieben werden, zudem ist stets auf die korrekte Polung zu achten. Das kurze Beinchen ist der Minus-Pol, das Lange der Plus-Pol. Zur zusätzlichen Kontrolle ist stets das Minus-Symbol an der Kondensatorhülle aufgedruckt. Darüber hinaus kennzeichnet eine schwarze Linie vielfach den Minus-Pol, sodass Verwechslungen bei den verschiedenen Gehäusetypen so gut wie ausgeschlossen sind.

Kondensatorberechnungen:
Ladezeit:
Die Ladezeit eines Kondensators hängt von dessen Größe sowie vom Widerstand ab, der dem Kondensator vorgeschaltet ist. Nun wird ein Kondensator nicht linear verlaufend geladen, sondern anfangs schnell, dann immer langsamer gefüllt.
Zum Berechnen der Ladezeit werden Zeitkonstanten benötigt. Sie geben an, welchen Ladezustand der Kondensator nach dem Verstreichen einer Zeitkonstante besitzt.
Die Formel zum Berechnen der Zeitkonstante t (tau) lautet:
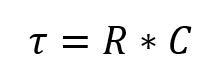
In der Praxis werden fünf Zeitkonstanten benötigt, um einen Kondensator zu laden beziehungsweise zu entladen. Zum Berechnen der Zeit, die zum Laden eines Kondensators nötig ist, wird daher folgende Formel verwendet:
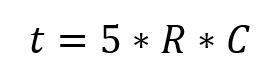
Angenommen, ein Kondensator von 10 µF wird über einen Widerstand von 1 Megaohm mit 30 V geladen, dann ist dieser nach dieser Zeit vollständig geladen:
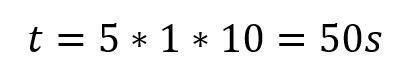
Fast eine Minute muss gewartet werden, bis der Kondensator voll ist. Der hohe Widerstand ist somit eine echte Bremse. Je mehr Kapazität der Kondensator hätte, desto länger würde es dauern, diesen voll aufzuladen. Die Spannung hingegen spielt bei der Ladezeit keine Rolle.
Entladezeit:
Die Entladezeit ist ebenso wichtig wie die Ladezeit. Wer diese berechnen kann, ist in der Lage, einen Kondensator gezielt für Steuerungsaufgaben einzusetzen, bei denen es darum geht, eine Abfallverzögerung zu realisieren.
Auch hier kommt die Formel für die Zeitkonstante zum Einsatz:
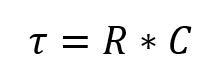
Ein Kondensator mit einer Kapazität von 100 µF wird, wenn er mit einem Widerstand von 1 kOhm verbunden ist, nach dieser Zeit entleert sein:
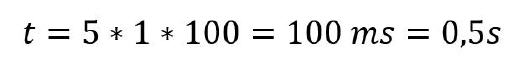
Der Kondensator ist demnach nach einer halben Sekunde leer. Es muss berücksichtigt werden, dass auch beim Entladen eines Kondensators fünf Zeitkonstanten benötigt werden, bis dieser völlig entleert ist. Aus diesem Grund steht wiederum die Zahl 5 in der obigen Formel.
Wird nun ein größerer Widerstand verwendet, so steigt natürlich auch die Zeit, bis der Kondensator völlig entladen ist. Bei einem 10 kOhm-Widerstand erhöht sich die Zeitkonstante auf 1s, was bewirkt, dass der Kondensator erst nach fünf Sekunden völlig entleert ist.
Nun kann man selbstverständlich auch den Strom berechnen, der während des Verstreichens der einzelnen Zeitkonstanten noch zur Verfügung steht. Dies ist nützlich, um ganz gezielt die Kondensator- und Widerstandgröße zu bestimmen, um ein gewünschtes Abfallverhalten zu erreichen.
Stromverlauf beim Entladen:
Um den Verlauf des Stromabfalls berechnen zu können, muss die Entladestromstärke ic berechnet werden.
Dies geschieht über die Formel:
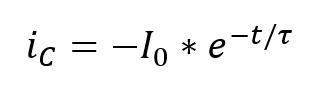
Es bedeuten:
I0 = Anfangsstromstärke
e = 2,71828 (Basis der natürlichen Logarithmen)
t = Zeit
(tau) = Zeitkonstante
Es geht jedoch auch einfacher. In der Praxis wird davon ausgegangen, dass sich nach der Zeitkonstanten t (tau) der Strom um rund 37 Prozent vom Vorgängerwert reduziert. Angenommen, ein Kondensator von 100 µF Kapazität wird mit 60 V betrieben und über einen Widerstand von 1 kOhm entleert, dann kann kann folgende Berechnung zum Verlauf des Stromabfalls angestellt werden:

Es zeigt sich, dass nach fünf Zeitkonstanten fast kein Strom mehr fließt. Der Kondensator ist somit fast vollständig entladen.
Über diese Berechnung kann somit eine Aussage getroffen werden, wie viele Zeitkonstanten verstreichen müssen, damit beispielsweise ein Relais umschaltet. Hat dieses zum Beispiel einen Haltestrom von 10 mA, so wird es kurz vor dem Verstreichen der zweiten Zeitkonstante umschalten.
Energiespeicherung:
Besonders interessant ist die Frage, wie viel Energie eigentlich ein Kondensator speichern kann. Die Antwort liefert folgende Formel:
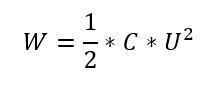
Angenommen, der Kondensator besitzt eine Kapazität von C=100 µF und wird mit U=110 V Gleichspannung geladen, dann ergibt sich:
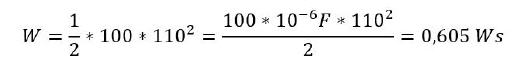
Praktischer Schaltungsaufbau:
Wie erwähnt, eignet sich der Kondensator dazu, eine Abfallverzögerung zu verwirklichen. Dadurch kann ein Stromausfall überbrückt oder eine gezielte Wirkung, etwa das langsame Verlöschen einer LED erreicht werden. Wie nachfolgender Schaltplan zeigt, ist so eine Schaltung kein Hexenwerk.
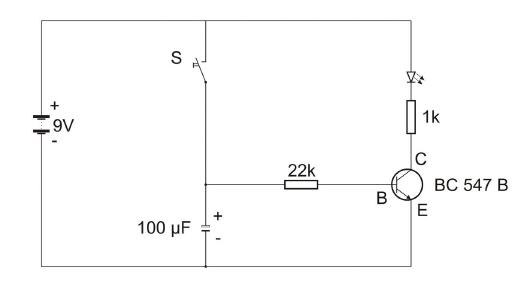

Wie sich zeigt, brennt die LED noch rund 15 Sekunden weiter, nachdem der Schalter S kurz betätigt und danach wieder losgelassen wurde. Wird statt des 100 µF-Kondensators ein Kondensator mit 10 µF Kapazität eingesetzt, so verlischt die LED bereits nach rund 1,5 Sekunden. Somit kann sehr schön die Wirkung unterschiedlich großer Kondensatoren beobachtet werden. Allerdings muss unbedingt darauf geachtet werden, ob der zu untersuchende Kondensator für eine Spannung von 9V geeignet ist. Die erlaubte Spannung ist unkritisch zu erkennen, da diese im Klartext auf dem Keramikkörper aufgedruckt ist.
Übrigens: Die Geschwindigkeit mit der die LED erlischt, kann auch durch einen größeren Widerstand wieder verlängert werden. Wird der 22 kOhm-Widerstand gegen einen 47 kOhm-Widerstand getauscht, so ist eine deutlich längere Brenndauer der LED feststellbar, die dann allerdings nicht mehr ganz so hell leuchtet.
Die Stromspeicherfähigkeit von Kondensatoren nutzen Fahrradhersteller, um damit für einige Minuten den Betrieb der Fahrradbeleuchtung aufrechtzuerhalten. Ein genauer Blick auf die Elektronik zeigt, dass für diesen Zweck ein verhältnismäßig großer Kondensator mit einer Kapazität von 1 Farad verwendet wird.

War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 5 - gesamt: 12846.
















































































