Das Iso-Toleranzsystem und dessen Berechnung
Dem Geheimnis der Passungsberechnung auf der Spur
Die Maße von Bauteilen müssen toleriert werden, um sicherzustellen, dass diese ohne Nacharbeit sicher montiert werden können. Damit dies problemlos zu bewerkstelligen ist, existiert die Norm ›DIN ISO EN 286‹, mit deren Hilfe sich Maße für Bauteile jeder Größe finden lassen, um je nach Aufgabenstellung bei deren Paarung Press-, Übergangs- und Spielpassungen zu bekommen. Die Ermittlung der fraglichen Toleranzen ist einfach, da die nötigen Werte einer Tabelle entnommen werden können. Doch wie kommen diese Werte zustande?
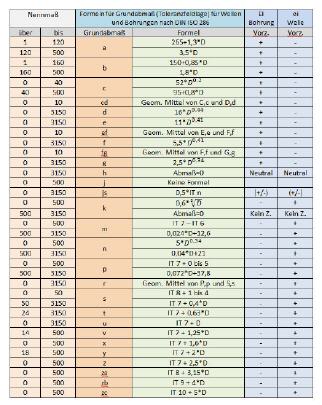
Bild 1: Formeln für Grundabmaße
Generationen von Facharbeitern, Technikern und Ingenieuren hantieren seit jeher sicher mit einem altbewährten Passungssystem, um für Konstruktionen jeder Art die optimalen Abmaße zu ermitteln. In der Regel wird das System ›Einheitsbohrung‹ verwendet, um, je nach Bedarf, zwei Bauteile über eine Press-, Übergangs-, oder Spielpassung zu verbinden.
Dabei sagt der Name ›Einheitsbohrung‹ schon, was hier die Grundlage bildet: Die Bohrung. Die Idee dahinter ist einfach: Es werden für bestimmte Bohrungsdurchmesser passende Reibahlen, etwa mit der Toleranzklasse ›H7‹ beschafft und die gewünschte Passungsart dann durch Abdrehen einer Welle auf das nötige Maß hergestellt.
Die Nutzung des Systems Einheitsbohrung hat praktische Gründe, denn es ist sehr viel leichter, unterschiedliche Durchmesser von Wellen anzufertigen, als die gleiche Zahl an Bohrungen herzustellen. Dazu kommen Kostengründe, denn die Beschaffung und Lagerung von Reibahlen ist weit kostengünstiger, als ein ähnliches System mit Wellen aufzubauen.
Natürlich ist es einfach, mittels Tabellen die nötigen Werte zu finden, um passende Toleranzen für den gewünschten Zweck zu finden. Reizvoller ist es jedoch zu verstehen, woher diese Werte kommen und wie die Formeln zu deren Berechnung aufgebaut sind.
Streng rationiert
Zunächst ist es wichtig zu wissen, dass man sich in der Technik auf ein bestimmtes System an Stufensprüngen geeinigt hat, um willkürliche Abstufungen in diesen Bereichen zu vermeiden. Egal ob Baugröße, Leistung, Drehmomente, Drücke oder Fördermengen betrachtet werden, in jedem Fall wurde mittels der DIN 323 sogenannte Normzahlen festgelegt, um die sich ergebenden Größenabstufungen zu begrenzen.
Diese Normzahlen sind in einer sogenannten geometrischen Reihe gestuft. Dies bedeutet, dass der Abstand einer Zahl zur vorherigen und nachfolgenden Zahl dem Verhältnis nach entsprechend stets konstant bleibt. Dieses zugrundeliegende Verhältnis wird als ›Stufensprung‹ bezeichnet. Dies bedeutet, dass jede Zahl sich durch Multiplikation der vorhergehenden Zahl mit dem Stufensprung ergibt. Eine geometrische Reihe hat dabei gegenüber einer arithmetischen Reihe den Vorteil, dass kleinere Werte feiner und größere Werte gröber gestuft sind. Dadurch ist die geometrische Reihe Ideal für Anwendungen in der Technik, insbesondere eben zur Anfertigung von Passungen.
Es sind vier Grundreihen genormt: R5, R10, R30 und R40. Dabei steht der Buchstabe ›R‹ natürlich für das Wort ›Reihe‹, während die Zahl angibt, wie viele Stufungen vorgenommen werden. R5 ist daher eine wesentlich gröbere Reihe als R40, da der zugrundeliegende Wertbereich von eins bis zehn lediglich fünf Abstufungen erhält und nicht 40.
Der gesuchte Abstand zwischen den einzelnen Stufen wird mit den Formeln in Bild 2 berechnet. Man sieht, dass bei der Reihe ›R5‹ aus der Zahl 10 die fünfte Wurzel gezogen wird, während bei der Reihe ›R40‹ die 40igste Wurzel aus der gleichen Zahl gezogen wird. Im ersten Fall bekommt man als Ergebnis 1,584893, im zweiten Fall den Wert 1,0592537. Diese Ergebnisse werden auf 1,6 beziehungsweise 1,06 gerundet.

Bild 2: Grundformeln
Runden nur nach DIN
Zum Berechnen von Passungen via Tabellenkalkulation oder Taschenrechner sollte das Runden jedoch unterbleiben, damit keine groben Abweichungen von den in Tabellenbüchern stehenden Werte erfolgen. Daher immer die volle Rechengenauigkeit nutzen, um korrekte Berechnungen mit Reihen durchführen zu können. Das Ergebnis anschließend auf eine Stelle hinter dem Komma runden, um bei der anschließenden Weiterverwendung des eben ermittelten Werts annähernd korrekte Werte zu erhalten. Wer sich nun die Frage stellt, wozu Reihen überhaupt nötig sind, erhält die Antwort im nächsten Abschnitt.
Reihen sind unter anderem für Passungstabellen und Oberflächenqualitäten wichtig. Ein Blick in ein Tabellenbuch offenbart, dass Reihen beispielsweise bei der Bestimmung von Bereichsklassen für den Mittenrauwert Ra genutzt werden. Die Rauheitsgrenzwerte 1.6, 3.2, 6.3, 12.6, 25 und 50 sind mit Hilfe der aus Bild 2 bekannten Formeln zur Berechnung von Reihen ermittelt worden. Das gleiche Prinzip wird zur Festlegung der Größe von Toleranzfeldern, genauer gesagt, von Grundtoleranzfeldern genutzt.
Nur ist es hier nicht so offensichtlich, wo sich dort die Reihen verstecken. Die Antwort ist: Sie dienen bei der Berechnung von Toleranzfeldern als Multiplikationsfaktor ›K‹, der noch näher erläutert wird. Reihen sind eine wichtige Voraussetzung zur Berechnung der Toleranzen. Diese werden jedoch erst ganz am Ende einer Berechnungskette benötigt, um schlussendlich zur gesuchten Toleranzfeldgröße zu kommen. Am Anfang dieser Rechenkette steht zunächst die Berechnung des Geometrischen Mittels eines gegebenen Nennmaßbereichs, in dem sich das Maß befindet, zu dem die Toleranzfeldgröße berechnet werden soll.
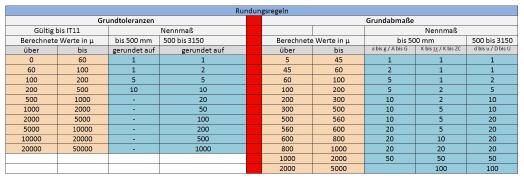
Bild 3: Rundungsregeln
Zusammenhänge erkennen
Die Formel zum Berechnen des Geometrischen Mittels ›D‹ zeigt wiederum Bild 2. Der mit dieser Formel ermittelte Wert wird genutzt, um den sogenannten Toleranzfaktor ›i‹ zu berechnen, dem die direkt darunterstehende Formel zugrunde liegt. Diese Formel ist gültig für die Toleranzgrade 5 bis 18. Diese Toleranzgrade sind mit den Werten der berechneten Reihe verknüpft. So wird beispielsweise dem Toleranzgrad 7 der Wert 16 und dem Toleranzgrad 11 der Wert 100 zugeordnet.
Wie erläutert, fungieren die Reihenwerte als Multiplikationsfaktoren K zur Berechnung der Grundtoleranz. Die Grundtoleranz ›T‹ entspricht der Größe des Toleranzfeldes, in dessen Grenzen sich das Ist-Maß des angefertigten Werkstückes befinden muss. Die Grundtoleranz T wird berechnet, indem der Toleranzfaktor ›i‹ mit dem Faktor ›K‹ multipliziert wird.
Ein Beispiel soll diesen Sachverhalt erläutern: Für die Wellenpassung 14 g6 ist die Grundtoleranz zu berechnen. Der Rechenweg ist in Bild 4 ersichtlich. Wie zu erkennen ist, beträgt das Geometrische Mittel für den Bereich 10 bis 18, in dem sich diese Bohrungsgröße befindet, 13,4164. Wird dieser Wert zugrundegelegt, so errechnet sich ein Toleranzfaktor von 1,08269. Diese Zahl wird nun mit dem Reihenwert 10 multipliziert. Das Ergebnis beträgt 10.8269, welches normgerecht auf 11 aufgerundet wird. Ein Vergleich mit einem Tabellenbuch zeigt, dass dieser Wert korrekt ist.
Damit die Lage stimmt
Was jetzt noch fehlt, ist die Lage des eben berechneten Toleranzfeldes beziehungsweise des Grundabmaßes zur Nulllinie. Die gestufte Lage der Grundabmaße zur Nulllinie ist leider nur unter Zuhilfenahme einer ganzen Reihe von Formeln zu ermitteln, die in Bild 1 zu finden sind. Wie zu sehen ist, wird die Lage der Grundabmaße mit Buchstaben angegeben, denen jeweils eine Formel zugeordnet ist, mit deren Hilfe die Lage des Toleranzfeldes berechnet werden kann. Dieser Wert wird für Bohrungen mit dem Kürzel ›ES‹ und für Wellen mit dem Kürzel ›es‹ gekennzeichnet.
Wie aus der Tabelle ersichtlich ist, lautet die Formel zum Berechnen der Toleranzfeldlage für eine Welle mit dem Durchmesser 14 g6 wir folgt: ei=2,5*D0,41. Das Kürzel ›ei‹ steht für den Abstand von der Nulllinie zum Beginn des Toleranzfeldes. Was als „Beginn“ des Toleranzfeldes gewertet wird, hängt von dessen Lage ab. Hier muss das in der Norm festgelegte Vorzeichen beachtet werden, um die Berechnung korrekt weiterzuführen. Hier entscheidet sich, ob das Toleranzfeld seinen nach Norm korrekten Platz zur Bezugslinie einnimmt. Der Burchstabe ›D‹ steht, wie bereits bekannt, für das Geometrische Mittel des Nennmaßbereichs 10 bis 18.
Gewusst wie
Die Berechnung (siehe Bild 4) ergibt, dass das Grundabmaß gerundet sechs Mikrometer beträgt. Das zu berücksichtigende Vorzeichen ist für den Buchstaben ›g‹ negativ, was bedeutet, dass das Grundabmaß um diesen Betrag unterhalb des Nennmaßes liegt. Von dieser Position aus wandert das Toleranzfeld nach unten, bis es eine Größe von 11 Mikrometer besitzt. Dieser Wert wurde bereits im ersten Rechenschritt ermittelt.
Nun ist es ein Leichtes, das zulässige Höchstmaß für die Welle GoW sowie das Mindestmaß GuW zu berechnen. Die Berechnung ist ebenfalls in Bild 4 ersichtlich. Auf diese Weise lassen sich alle Passungen ohne Tabellen berechnen. Allerdings muss immer darauf geachtet werden, dass sowohl für die Grundtoleranzen, als auch für die Grundabmaße je nach Größe der berechneten Werte unterschiedliche Rundungsregeln gelten. Nur wenn diese beachtet werden, sind die ermittelten Werte nach Norm korrekt.
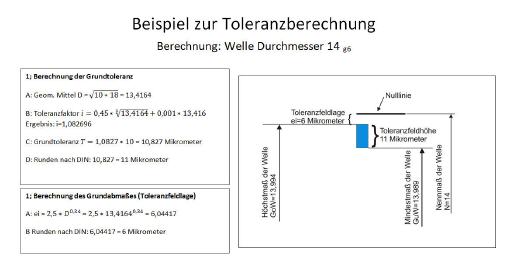
Bild 4: Beispielberechnung
Download
Diesen Artikel können Sie hier im PDF-Format [1.888 KB] herunterladen.
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 7 - gesamt: 27596.















































































