Rechnen mit den Napierschen Stäben
Der Taschenrechner des Mittelalters
Bevor der Taschenrechner Einzug in Schule, Werkstatt und Büro hielt, mussten sich die Menschen anderweitige Rechenhilfen besorgen, um lange Zahlen relativ einfach handzuhaben. Eine dieser Hilfen ersann der schottische Mathematiker John Napier. Dessen Rechenstäbe leisten Erstaunliches. Zeit, das verschüttete Wissen rund um diese Stäbe wieder auszugraben.

Es ist schade, dass viele wichtige Errungenschaften im Laufe der Zeit wieder verblassen, wenn eine bessere Erfindung den Platz einnimmt. Dieses Schicksal hat auch die Rechenstäbe von John Napier ereilt. Obwohl sie genial einfach handhabbar sind und mit ihnen selbst größte Zahlen mühelos multipliziert werden können, ist das Wissen um sie nur mehr einem kleinen Kreis von Experten bekannt. Das zugrundeliegende System ist jedoch derart genial, dass es sich lohnt, darüber Bescheid zu wissen.
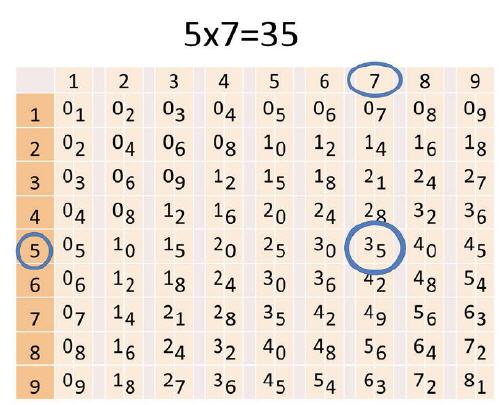
In den Rechenstäben ist das Einmaleins enthalten
Um die Napierschen Rechenstäbe, auch Nepersche Stäbe genannt, zu verstehen, ist nur wenig Zeitaufwand nötig. Das Geheimnis liegt darin zu verstehen, dass jeder Stab einen Teilbereich des kleinen Einmaleins beherbergt und daher die kleinste Menge an Stäbchen neun beträgt, um die Zahlenreihe von eins bis neun abzudecken. Es können beliebig viele Stäbe aneinandergereiht werden, sodass selbst längste Zahlen handhabbar sind. Die Aussage ›beliebig viele Stäbe‹ bedeutet natürlich, dass jeder Stab eine unbegrenzte Zahl an Klonen haben kann, um jede beliebige Zahl darzustellen. Dies bedeutet, dass mit Neperschen Stäben Berechnungen möglich sind, die mit so manchem Taschenrechner nicht möglich sind!
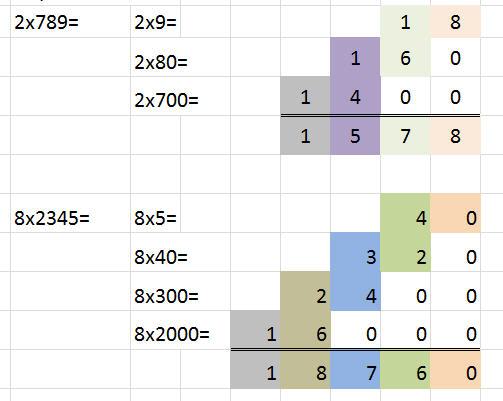
Die Rechenstäbe folgen simpler Mathematik
Damit Berechnungen ausgeführt werden, ist es noch notwendig, auf der linken Seite einen Stab mit den Multiplikatoren anzulegen. Die Multiplikanden bringt jeder Stab bereits mit. Diese stehen ganz oben auf dem jeweiligen Rechenstab. Wenn man nun die Stäbe genau ansieht, dann erkennt man, dass das kleine Einmaleins dort niedergeschrieben steht. Zum Beweis sollen die Rechnungen 2x2; 5x7 und 9x8 herangezogen werden. Wie man unschwer erkennen kann, stehen die Ergebnisse an der jeweiligen Stellen auf den Stäbchen.
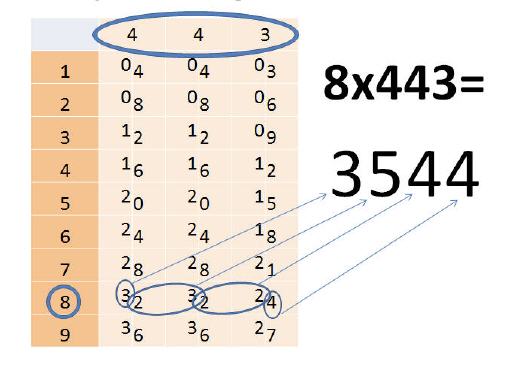
Größte Zahlen sind einfach berechenbar
Da die Stäbchen einzeln beweglich sind, können diese zu jeder beliebigen Zahl aneinandergereiht werden. Wenn zum Beispiel die Zahl 443 mit 8 multipliziert werden soll, dann benötigt man lediglich zwei Stäbchen von der ›4‹ und ein Stäbchen von der ›3‹. Sobald diese aneinandergereiht sind, kann die Berechnung starten. Dazu ist es nur nötig, die jeweils direkt gegenüberstehenden Zahlen zu multiplizieren und alleine stehende Zahlen direkt auf ein Blatt Papier zu schreiben.
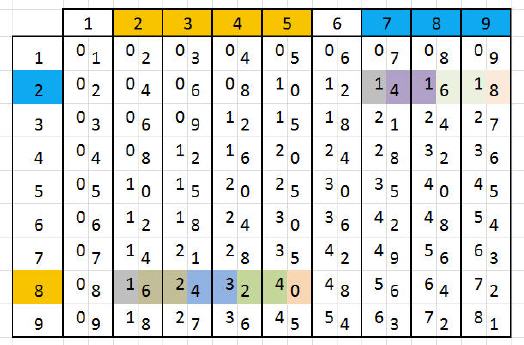
Rechenstabsimulation per Tabellenkalkulation
Dieses Schema, das man übrigens auch mit jeder Tabellenkalkulation einfach simulieren kann, gilt für jede Zahl und wenn sie noch so groß ist. Dieses System hat der „Uhrmacher Gottes“, Philipp Matthäus Hahn zum schnelleren Rechnen sogar auf eine Rechentrommel übertragen und später in seinen Rechenmaschinen genutzt. Wer sich dafür interessiert, sei an das Philipp-Matthäus-Hahn-Museum in Albstadt-Onstmettingen verwiesen.
Video
Zum umfassenden Verständnis der Rechenstäbe ist das nachfolgende Video sehr zu empfehlen.
Download
Diesen Artikel finden Sie hier im PDF-Format [504 KB]
.
Mehr Informationen:
 |
Philipp-Matthäus-Hahn-Museum |
 |
Albert-Sauter-Str. 15 (Kasten) |
 |
72461 Albstadt |
 |
Stadtteil Onstmettingen |
 |
Tel.: 07432/23280 |
 |
Öffnungszeiten: Mi, Sa, So, Fei 14-17 Uhr |
 |
Eintritt: 2,00 EUR |
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 7 - gesamt: 7644.















































































