Rechnen mit Binärzahlen
Der erste Schritt zum Relaisrechner
Dass Computer mit Binärzahlen rechnen, ist mittlerweile nahezu Allgemeinwissen. Weniger bekannt ist, wie dies vonstattengeht. Das einfache Beispiel der Umwandlung von drei Dezimalzahlen in ihre Binärwerte sowie deren anschließende Addition vermittelt Einblicke in die Welt der Computer, von wo aus der Bau eines einfachen Relaisrechners à la Zuse nicht mehr weit ist.

Zuse Z11
Computer sind eine faszinierende Errungenschaft der Menschheit, die vielen Menschen unheimlich vorkommen, weil sie die Technik dahinter nicht verstehen. Der Grund ist vielfach, dass, anders als bei mechanischen Maschinen, keine Zahnräder, Hebel und Federn in Bewegung beobachtet werden können, die die Funktion der jeweiligen Maschine begreiflich machen. Es bietet sich daher an, die Idee von Konrad Zuse aufzugreifen, dessen Rechner Z3, Z4 oder Z11 auf der Relaistechnik fußten. Derartigen Rechnern kann beim Arbeiten zugesehen werden, was für das Verständnis der Arbeit eines Computers von großem Wert ist.
Relaisrechner machen durch das Öffnen und Schließen von Kontakten sehr anschaulich das Binärprinzip deutlich, das auf den Zahlen 0 und 1 fußt. In einem Relais ergibt sich durch eine 0 ein offener Kontakt, wodurch ein Stromfluss unterbrochen wird. Die Zahl 1 hingegen bedeutet einen geschlossenen Kontakt, durch den nun Strom fließen kann.

Relais einer Z11
Dieses Prinzip ist auch in Lochstreifen, Kernspeichern sowie Lochkarten zu finden und lässt sich dazu nutzen, Daten zu speichern sowie Berechnungen durchzuführen.

Lochkarte und Lochstreifen

Magnetkernspeicher
Um mit einem Computer Berechnungen durchzuführen, ist es nötig, die uns gewohnten Dezimalzahlen in Binärzahlen umzuwandeln. Die Umwandlung ist zumindest bei kleinen Zahlen recht einfach, da das Binärsystem, beginnend mit der Null, eine Ansammlung von Nullen und Einsen ist, die nach folgendem System angeordnet werden:
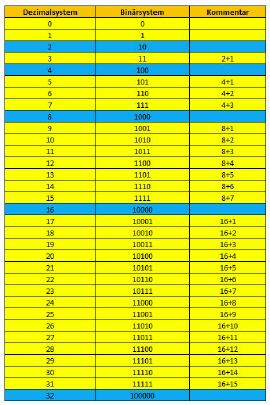
Dezimalzahl in Binärzahl umwandeln
Man beachte Folgendes:
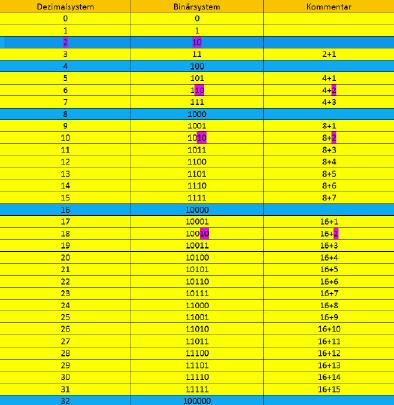
Das System zeigt, dass jeweils von rechts nach links im Binärsystem eine 1 dazukommt, wenn sich der Wert der Dezimalzahl um eins erhöht.
Es gibt einen einfachen Weg, durch simple Division aus jeder beliebigen Dezimalzahl die Binärzahl zu ermitteln. Dazu wird die Zahl solange durch zwei dividiert, bis als Ergebnis eine Null herauskommt. Der jeweilige Rest der einzelnen Divisionsschritte bildet dabei – von unten korrekt aneinandergereiht – die gesuchte Binärzahl.
Beispiel:
Umwandlung der Dezimalzahl 28 in eine Binärzahl:
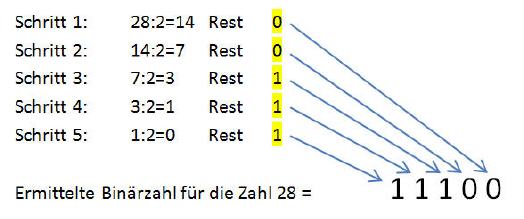
Ermittelte Binärzahl für die Zahl 28 = 1 1 1 0 0
Wichtig: Die Restwerte müssen, beginnend mit dem letzten Wert (in diesem Fall Schritt 5), von links nach rechts aneinandergefügt werden, damit die Binärzahl korrekt ermittelt wird.
Binärzahlen addieren:
Sind nun Dezimalzahlen in ihre jeweiligen Binärzahlen umgewandelt worden, so können Computer diese Werte nutzen, um sie beispielsweise zu addieren. Dieser Prozess ist einfach nachzuvollziehen, wenn die Vorgehensweise verstanden wurde. Sollen beispielsweise die Zahlen 28, 29 und 30 addiert werden, so ist wie folgt vorzugehen:
Zunächst die Binärzahlen der Dezimalzahlen ermitteln:
28 = 11100
29 = 11101
30 = 11110
Dann die Binärzahlen addieren:
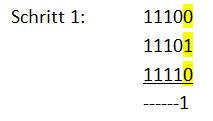
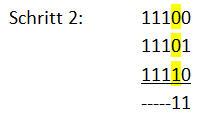
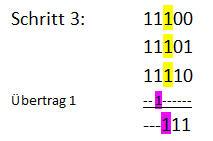

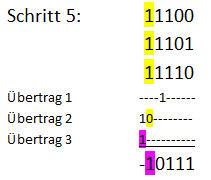


Ergebnis der Addition von 28+29+30 = 87. Diese Zahl besitzt den Binärwert 1010111.
Möchte man das Ergebnis der Umwandlung einer Dezimalzahl in eine Binärzahl überprüfen, so ist dies rasch umgesetzt.
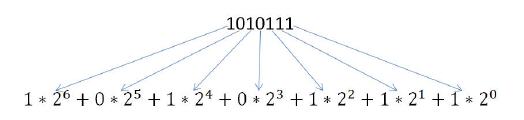
Das Ergebnis dieser Berechnung ist 87 und dokumentiert, dass die Umwandlung der Zahl 87 in ihre Binärzahl korrekt erfolgte.
Einige Hinweise zur Addition von Binärzahlen:
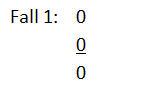
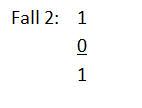
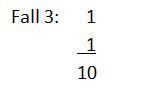
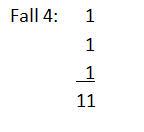
Werte, die größer als 0 oder 1 sind, müssen als Übertrag behandelt werden, damit Binärzahlen korrekt berechnet werden.
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 4 - gesamt: 2727.















































































