Kreisförmige Bewegung in Geogebra
Animation einer Raddrehung
Pendelbewegungen sind in Geogebra relativ leicht umzusetzen. Doch schon die Animation eines in 2D dargestellten Rades, in dem Bohrungen eingebracht sind, bereitet Probleme. Eine um die Radachse verlaufende, kreisförmige Bewegung des Rades wird erst dann richtig dargestellt, wenn eine wichtige Regel beachtet wird, damit die Simulationsberechnung durch Geogebra korrekt erfolgt.
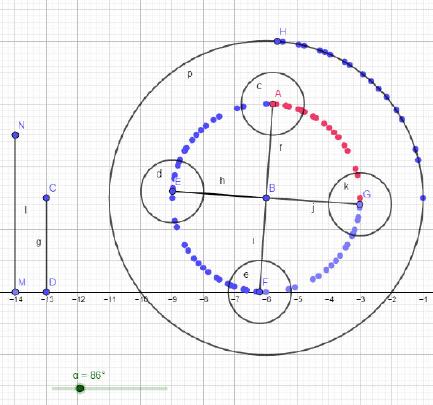
Die Simulation eines Rades mit vier darin eingelassenen Bohrungen ist für langjährige Geogebra-Nutzer keine große Hürde, jedoch sehr wohl für Einsteiger, da Geogebra eine Hürde bereithält, die nicht sein müsste. Doch zunächst gilt es, die zu animierenden Elemente zu zeichnen sowie einen Schieberegler zu platzieren.
Das Ergebnis sollte etwa so aussehen:
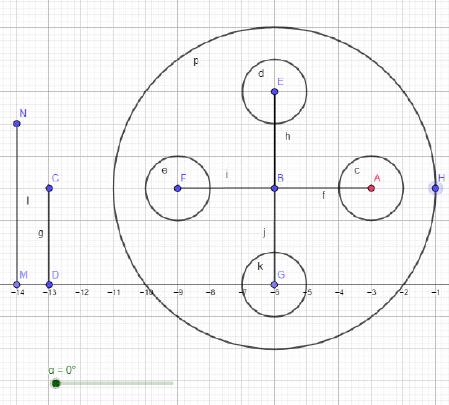
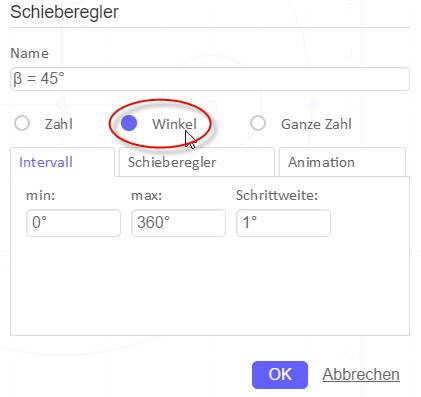
In Geogebra ist besonders praktisch, dass sich mittels Schieberegler Elemente sehr einfach neu positionieren lassen. Die funktioniert auch mit Winkelwerten, wenn der Schieber beim Einrichtevorgang entsprechend eingestellt wird.
Anders als bei einem Pendel kommen in diesem Beispiel gleich vier, wenn Punkt ›H‹ mitgezählt wird, gar fünf drehende Elemente vor, deren Position stets neu berechnet werden muss, wenn sich der Wert des Schiebers ändert.
Und hier kommt nun eine Eigenheit von Geogebra zum Tragen, an der viele Einsteiger schier verzweifeln:
Obwohl der Schieber augenscheinlich in Grad funktioniert, müssen per Formel getätigte Winkelmanipulationen zwingend in Bogenmaß vorgenommen werden, soll die Animation korrekt ablaufen!
Die Formel zum Umwandeln eines Gradwertes in einen Bogenmaßwert lautet:
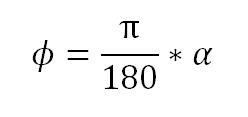
Soll ein Bogenmaßwert wieder in Grad umgerechnet werden, so ist folgende Formel anzuwenden:
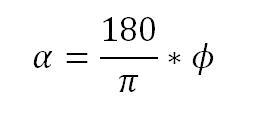
Für Punkt A sind die für eine Animation nötigen Start-Koordinaten mühelos zu ermitteln.
Die Formel lautet für die X-Achse:
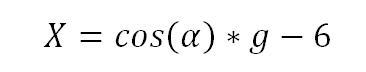
und für die Y-Achse:
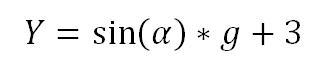
In der Eingabezeile für die Definition von Punkt A muss demnach stehen:
(cos(α) g - 6, sin(α) g + 3)
Hier ist zu beachten, dass Geogebra das Malzeichen – mathematisch korrekt – ausblendet.
Sollen nun die Start-Koordinaten des um 90 Grad zu Punkt A versetzten Punktes E ermittelt werden, so muss zur obigen Formel der Startwinkel in Bogenmaß hinzugefügt werden. Da ein Wert in Bogenmaß für an Grad gewohnte Nutzer wenig Aussagekraft hat, sollte in der Formel der Grad-Wert genutzt und direkt in Bogenmaß umgewandelt werden.
Die Formeln für beide Koordinatenwerte lauten:
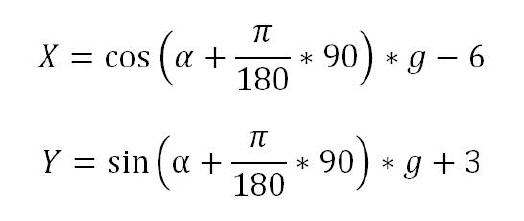
In der Definitionszeile für Punkt E muss demnach stehen:
(cos(α + 3.14 / 180 * 90) g - 6, sin(-α + 3.14 / 180 * 90) g + 3)
Folgendes Bild für die X-Koordinate soll den Sachverhalt näher erläutern:
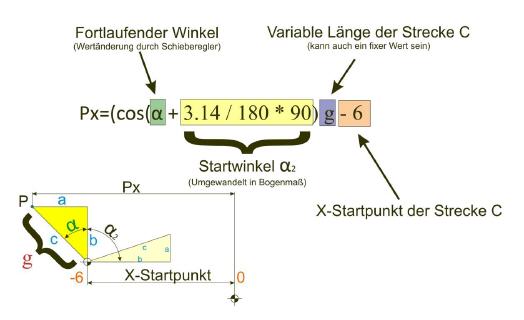
Erklärungsbedürftig ist noch die Variable ›g‹. Hier handelt es sich eigentlich um die Strecke c beziehungsweise um die Hypotenuse des zu berechnenden Dreiecks. Diese Variable wird durch eine eingezeichnete Strecke repräsentiert, deren Änderung sich unmittelbar auf die Simulation auswirkt.
Alternativ kann auch ein fester Wert anstelle der Variablen g verwendet werden, was jedoch mit einer Verringerung der Manipulationsmöglichkeiten während einer Simulation einhergeht.
Nachfolgend nun die Formeln zum Berechnen aller Koordinatenpunkte:
Punkt A: 0 Grad: (cos(α) g - 6, sin(α) g + 3)
Punkt E: 90 Grad: (cos(α + 3.14 / 180 * 90) g - 6, sin(-α + 3.14 / 180 * 90) g + 3)
Punkt F: 180 Grad: (cos(-α + 3.14 / 180 * 180) g - 6, -sin(-α + 3.14 / 180 * 180) g + 3)
Punkt G: 270 Grad: (cos(α + 3.14 / 180 * 270) g - 6, sin(-α + 3.14 / 180 * 270) g + 3)
Für Punkt H ist das gleiche Schema anzuwenden. Jedoch sind dessen Mittelpunktskoordinaten mithilfe der Variablen l zu berechnen, die ebenfalls durch eine Strecke repräsentiert wird.
Die Formel lautet:
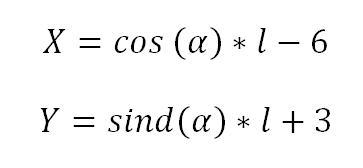
In der Definitionszeile für Punkt H muss demnach stehen:
(cos(α) l - 6, sin(α) l + 3)
Wird die Spuranzeige aller Punkte eingeschaltet, so kann verdeutlicht werden, dass sich alle Punkte korrekt um den Mittelpunkt B drehen.

War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 1 - gesamt: 7748.















































































