Das Spiel mit der Erdanziehungskraft
Der schiefe und der waagrechte Wurf
Der schiefe Wurf ist ein interessantes Stück Mathematik, das uns im Alltag und bei der Ausübung von Sport auf Schritt und Tritt begleitet. Ohne groß darüber nachzudenken sind wir in der Lage, die dazu passenden mathematischen Formeln anzuwenden und beispielsweise einen Ball mühelos einem Mitspieler zuzuwerfen. Wer die Formeln dazu kennt, kann das Wissen um den schiefen Wurf auch technisch nutzen.

Der schiefe Wurf wäre furchtbar einfach zu berechnen, wenn es keine Erdanziehungskraft gäbe. Im schwerelosen Raum bewegt sich ein Körper im einmal gewählten Winkel exakt auf einer Geraden weiter. Da wir uns nun jedoch auf der Erde befinden, die eine Anziehungskraft von 9,81m/s im Quadrat auf jeden Körper ausübt, überlagert sich die Bewegung eines in einem bestimmten Winkel geworfenen, auf einer Gerade wegfliegenden Körpers mit der Anziehungskraft der Erde.
Der vom Werfer in einem Winkel mit der Geschwindigkeit V0 weggeschleuderte Körper wird einer gleichmäßig beschleunigten Bewegung in Richtung Erdmittelpunkt ausgesetzt, wodurch dieser pro Streckenabschnitt einen bestimmten Wert Richtung Erde abgelenkt wird und so die Winkelgerade verlässt, auf der er sich ohne Erdanziehung befinden würde.
Da zwei Bewegungen gleichzeitig ablaufen, nimmt die Flugbahn des Körpers nun die Form einer Parabel ein, deren Gestalt je nach Startgeschwindigkeit und Abflugwinkel variiert.
Bei der Berechnung der Wurfweite werden die trigonometrischen Funktionen benötigt.
Da die Erdanziehung nur in der Y-Achse wirkt, kann der Weg in X-Richtung relativ einfach berechnet werden.
Die Formel lautet:
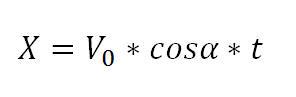
Aus der Formel geht hervor, dass die zurückgelegte Strecke ein Produkt aus Abschusswinkel α, Anfangsgeschwindigkeit V0 und Flugzeit t ist.
Fliegt beispielsweise ein Ball zwei Sekunden unter einem Winkel von 30 Grad mit einer Geschwindigkeit von 20 m/s so legt dieser eine Strecke von X=20*cos(30)*2=34,6 Meter zurück.
Zur Berechnung des Wegs in der Y-Richtung wird prinzipiell die gleiche Formel, diesmal jedoch mit der Sinusfunktion genutzt:
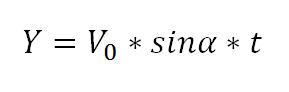
Würde der Ball im Weltraum ohne Schwerkrafteinfluss im Winkel von 30 Grad auf die schon erwähnten 20 m/s beschleunigt werden, so hätte dieser nach zwei Sekunden Flugzeit eine Höhe von Y=Vo*sin(30)*2=20 Meter erreicht.
Da jedoch die Erdanziehungskraft auf den Ball einwirkt, muss dieser Einfluss mathematisch berücksichtigt werden, indem die folgende Formel
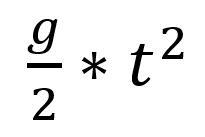
in die eben genutzte Formel eingearbeitet wird. Dies muss dergestalt erfolgen, dass vom berechneten Ergebnis der ursprünglichen Formel das Ergebnis des Einflusses der Erdanziehung abgezogen wird.
Die Formel für den Y-Weg lautet daher:
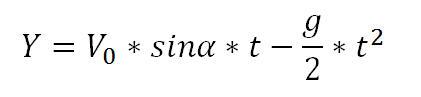
Der nun auf der Erde unter einem Winkel von 30 Grad mit einer Geschwindigkeit von V0 20 m/s geworfene Ball wird in zwei Sekunden einen Weg zurücklegen, der es erlaubt, eine Tonne in 34,6 Metern Entfernung exakt zu treffen, da die ursprünglich ohne Gravitationseinfluss errechnete Höhe nach dieser Zeit nahezu auf Null gesunken ist.
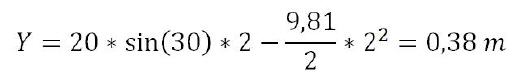
Unbewusst berechnen Sportler, die mit Bällen zu tun haben, die Wurfweite des Balls. Das „Gefühl“ für den Ball ist eigentlich eine mathematische Leistung des Gehirns, mit der Menschen in die Lage versetzt werden, Bälle oder andere Gegenstände im passenden Winkel auf die notwendige Geschwindigkeit zu beschleunigen, um ein gewünschtes Ziel zu treffen.
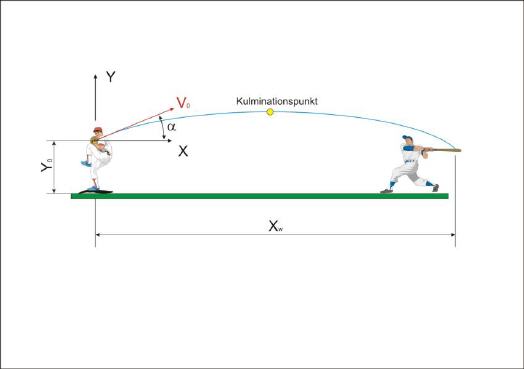
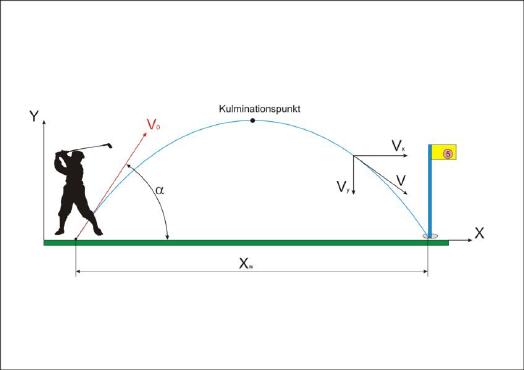
Dieses Wissen kann auch auf andere Weise genutzt werden. In erster Linie ist dabei an Rettungseinsätze mit dem Hubschrauber zu denken, um etwa in Überschwemmungsgebieten rettende Versorgungsgüter punktgenau aus einem Flugzeug oder Hubschrauber abzuwerfen.
Der waagrechte Wurf
Der waagrechte Wurf ist ein Sonderfall des schiefen Wurfes, da hier der Abwurfwinkel stets null Grad beträgt. Die Kenntnis und die Berechnung dieses Falles sind jedoch höchst interessant, wie vorhin bereits angedeutet.
Möchte ein Rettungsteam beispielsweise in 300 Meter Höhe (Sy) eine Last aus einem Hubschrauber abwerfen, der sich mit 90 km/h auf das Ziel zubewegt, so kann mit Kenntnis der passenden Rechenschritte dies relativ zuverlässig durchgeführt werden.
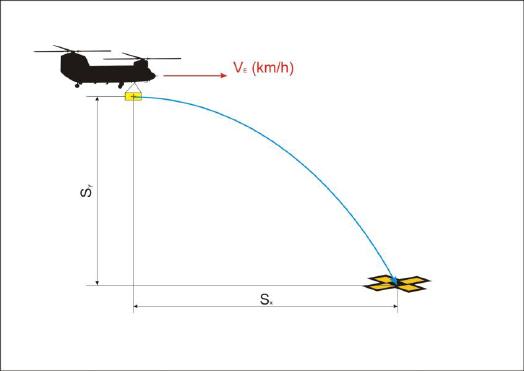
Zunächst ist die Geschwindigkeit des Hubschraubers in m/s umzurechnen. Dazu teilt man einfach den Geschwindigkeitswert durch 3,6 und erhält als Ergebnis die Geschwindigkeit in m/s. Ein mit 90 km/h dahinfliegender Hubschrauber legt demnach pro Sekunde 25 Meter zurück. Danach kann problemlos der Weg in X-Richtung (Sx) berechnet werden, um bei dieser Geschwindigkeit die Last nach dem Ausklingen exakt ins Ziel zu bekommen.
Die Formel dazu lautet:
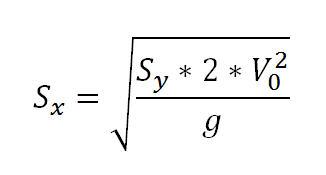
Nun noch die bekannten Werte eingeben:
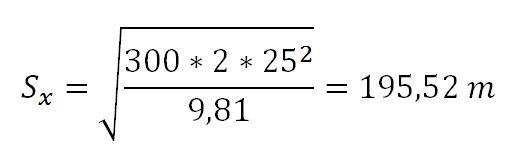
Der Hubschrauberpilot muss also 195,5 Meter vor dem Ziel die Last ausklinken, damit diese exakt ins Ziel fliegt. Um die Zeit zu berechnen, bis die Last im Ziel ist, muss folgende Formel zur Anwendung kommen:
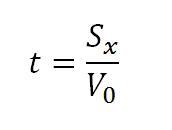
Hier ist ersichtlich, dass die Strecke X durch die Geschwindigkeit V0 dividiert wird, um die Flugzeit zu ermitteln.
Nun noch die Werte eingetragen, um das Ergebnis zu bekommen:
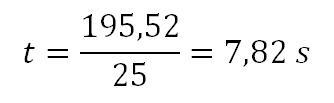
Die Last benötigt eine Flugzeit von knapp acht Sekunden, ehe sie am Ziel angekommen ist.
Natürlich stimmt das nicht ganz exakt, da der Widerstand der Luft noch nicht berücksichtigt ist. Dies soll jedoch das Thema eines vertiefenden Artikels sein.
Download:
Eine Excel-Tabelle zum Berechnen des schiefen Wurf können Sie hier herunterladen [107 KB] .
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 4 - gesamt: 7990.















































































