Schnittpunktberechnung Gerade-Gerade
Per Dreiecksberechnung zum Punkt
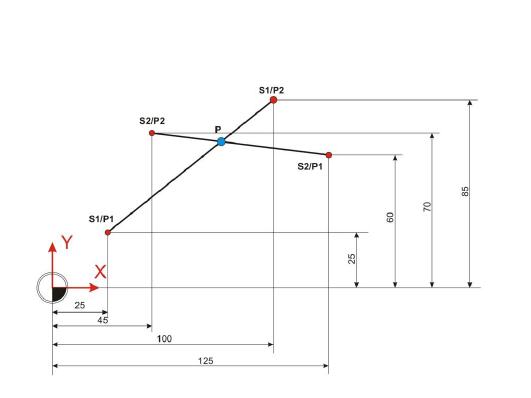
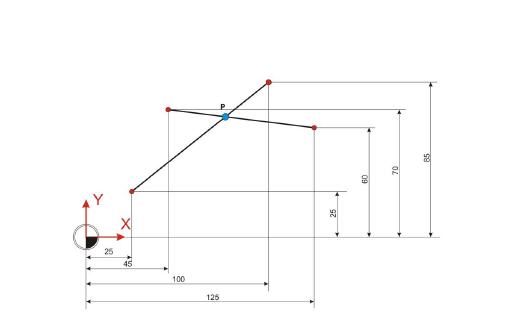
Auf den ersten Blick ist die Schnittpunktberechnung von zwei sich schneidenden Geraden problemlos machbar. Der unbedarfte Versuch zeigt jedoch, dass man ohne Rechenfertigkeiten am schiefwinkligen Dreieck nicht ans Ziel kommt.
Bevor dieses Manuskript durchgearbeitet wird, empfiehlt sich die Lektüre des Skripts ›Berechnung der Schnittpunkte zwischen zwei Kreisen‹, das hier zu finden ist. Erst mit dieser Grundlage kann an dieser Stelle sinnvoll weitergelesen werden, da sonst wesentliche Dinge unbekannt bleiben.
Folgende Beschreibung erhebt keinen Anspruch, den besten Rechenweg zur Berechnung von Radius und Kreismittelpunkt zu beschreiben, wenn zwei oder drei Punkte gegeben sind. Wie hinreichend bekannt, führen immer mehrere Wege ans Ziel. Nicht alle Wege sind jedoch für jeden gleichermaßen geeignet. Der vorgeschlagene Lösungsweg ist daher nicht unbedingt jedermanns Favorit. Er kommt jedoch den Fachleuten entgegen, die gerne die Dreiecksberechnung zur Lösung geometrischer Aufgaben heranziehen.
Schnittpunkt aus zwei gegebenen Geraden berechnen:
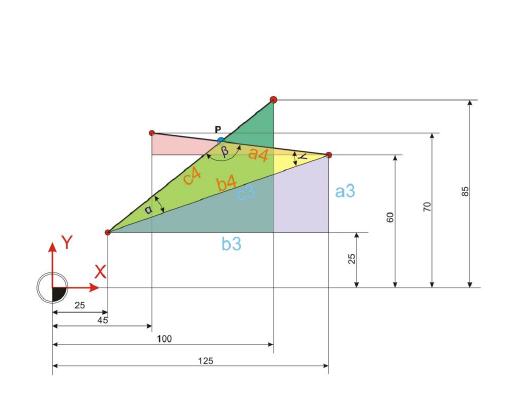
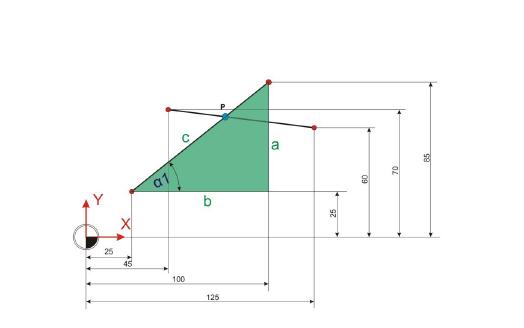
Im ersten Schritt der Berechnung des Schnittpunkts zweier Geraden ist es nötig, zunächst die Winkel der sich ausbildenden Dreiecke zu berechnen.
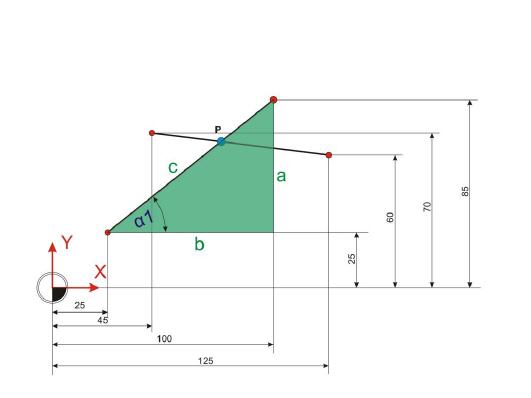
Winkel Alpha 1:
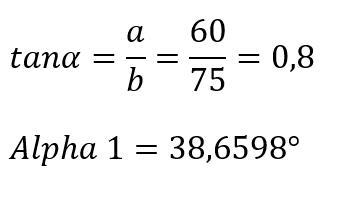
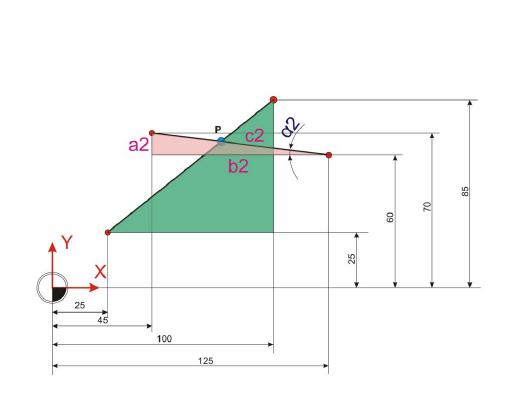
Winkel Alpha 2:
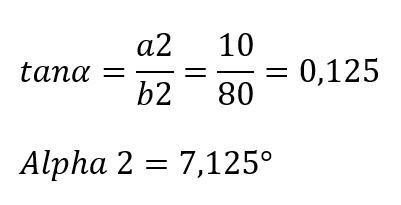
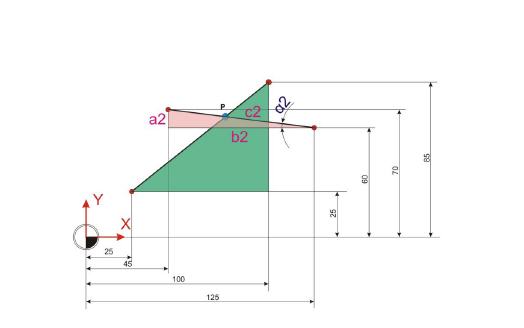
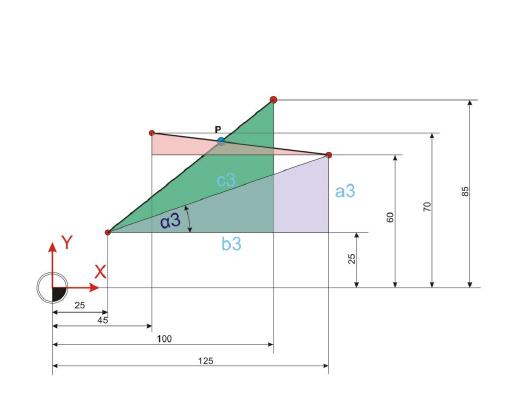
Winkel Alpha 3:
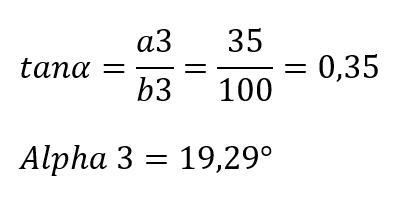
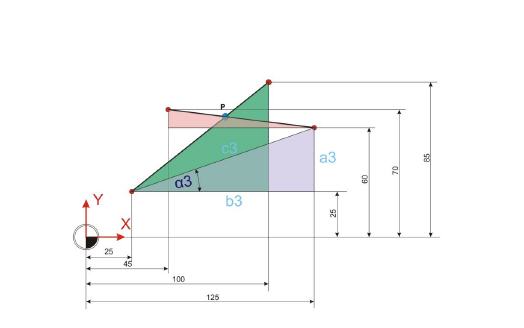
Werte im schiefwinkligen Dreieck berechnen:
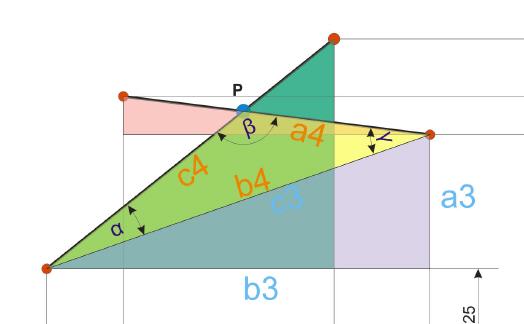
Die Berechnung der Winkel und Strecken im schiefwinkligen Dreieck sind der Schlüssel zur Ermittlung der Koordinaten von Punkt P. Dazu ist zunächst die Strecke b4 zu berechnen. Diese Strecke entspricht der Strecke c im pflaumenfarbenen, rechtwinkligen Dreieck.
Strecke b4:
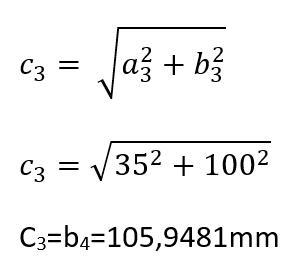
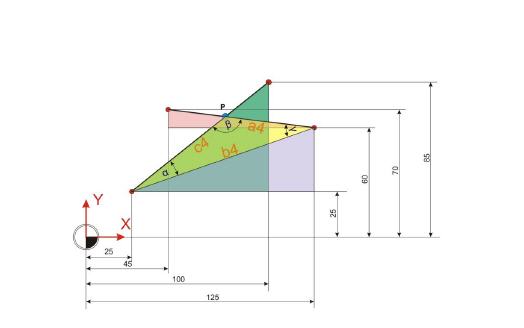
Als nächster Schritt bietet es sich an, den Winkel Gamma zu ermitteln. Dieser Winkel bildet sich aus der Summe der beiden Winkel Alpha 2 und Alpha 3. Dazu ist es wichtig zu wissen, dass Winkel im rechtwinkligen Dreieck entlang der Hypothenuse (c) gespiegelt werden und daher folglich sich auf der gegenüberliegenden Seite spiegelverkehrt abbilden.
Winkel Gamma:
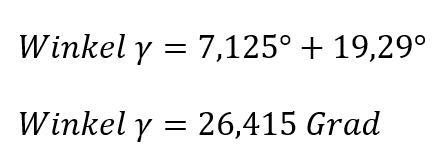
Der Winkel Alpha ist ähnlich einfach zu ermitteln. Dazu wird einfach der Winkel Alpha 3 vom Winkel Alpha 1 subtrahiert.
Winkel Alpha:
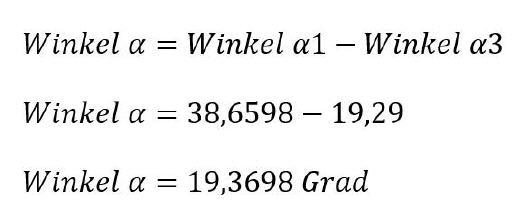
Nun ist auch die Ermittlung des Winkels Beta kein
Problem mehr.
Winkel Beta:
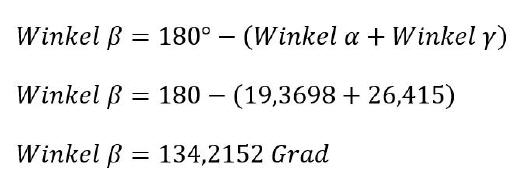
Im nächsten Rechenschritt gilt es, die Strecke c4 zu ermitteln. Wenn diese bekannt ist, dann sind alle Werte vorhanden, um die Koordinaten des Punktes P zu ermitteln.
Strecke c4:
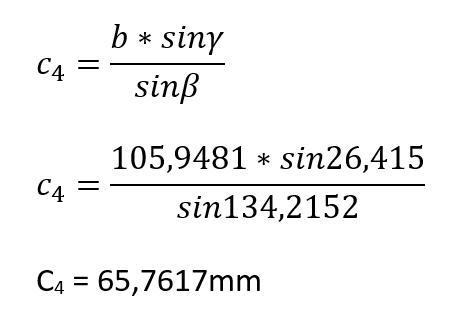
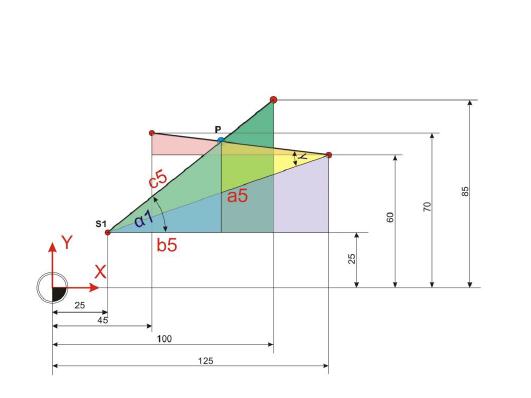
Nun sind die Koordinaten des Punktes P in greifbarer Nähe. Jetzt geht es nur mehr darum, die Strecken a4 und b4 in einem rechtwinkligen Dreieck zu ermitteln und die gewonnenen Werte zum Punkt S1 dazuzurechnen. Die Hypotenuse c5 entspricht der Strecke c4, die bereits ermittelt wurde.
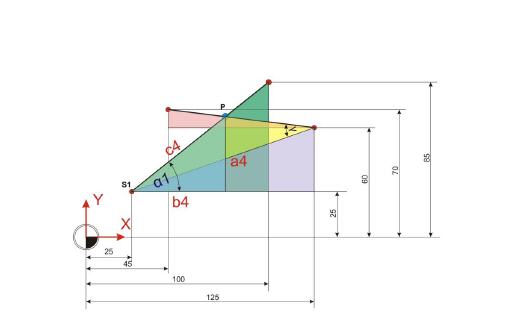
Ankathete a5:

Gegenkathete b5:

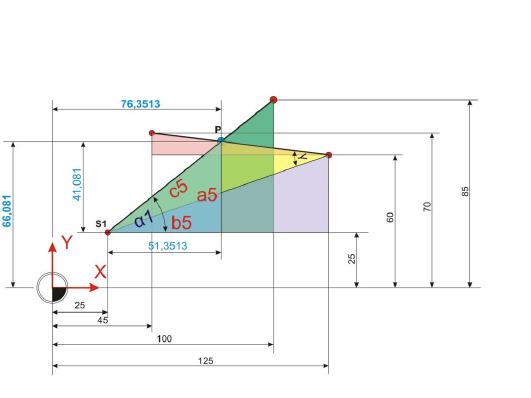
Nachdem nun alle Maße ermittelt sind, können die Koordinaten von Punkt P berechnet werden. Dazu werden die berechneten Werte einfach mit den Koordinaten des Punktes S1 entsprechend verarbeitet.
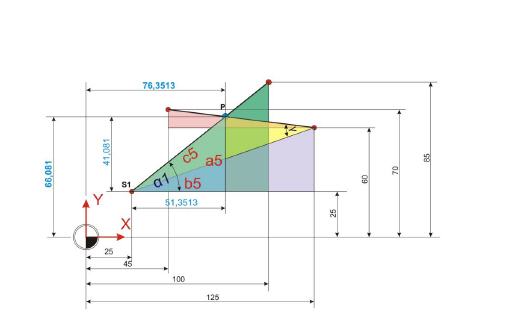
Schnittpunkt X:
SP-X = S1-X + b5
SP-X = 25 + 51,3513
SP-X = 76,3513mm
Schnittpunkt Y:
SP-Y = S1-Y + a5
SP-Y = 25 + 41,081
SP-Y = 66,081mm
Download:
Eine Excel-Tabelle zum Berechnen des Schnittpunkts zwischen zwei Geraden können Sie hier [1.054 KB] herunterladen.
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 5 - gesamt: 13898.