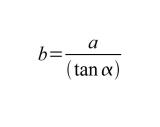Winkelfunktionen ohne Mühe verstehen
Anspruchsvolle Berechnungen leicht lösen
Winkelfunktionen sind nur auf dem ersten Blick ein abschreckendes Stück Mathematik. Das Geheimnis zu ihrem Verständnis liegt in der Art und Weise, wie man sie erklärt bekommt.
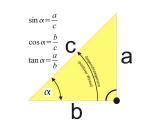
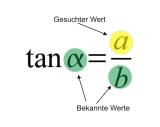
Sinus, Cosinus und Tangens nötigen alleine durch ihre Namen jedem Schüler eine gehörige Portion Respekt ab. Völlig zu Unrecht werde sie als unüberwindliche Hindernisse auf dem Weg zum Verständnis einer wunderbaren Mathematik angesehen. Das Geheimnis zu ihrer Beherrschung liegt vielmehr darin, sich nicht von der oft umständlichen Erklärung aus so manchem Pädagogenmund irre machen zu lassen. In dieser kleinen Abhandlung zu den Winkelfunktionen wird sich keine Zeile finden, wo von „Ankathete“ oder „Hypotenuse“ die Rede ist, da dies nur unnötiger Ballast auf dem Weg zum sicheren Umgang mit den Winkelfunktionen ist. Hier wird lediglich von den Buchstaben a,b und c die Rede sein. Darüber hinaus genügt es, sich drei Merksätze einzuprägen.
Drei Merksätze
- Positive Winkel verlaufen im Gegenuhrzeigersinn.
- Lediglich drei Grundformeln zum Berechnen aller unbekannten Werte im rechtwinkligen Dreieck müssen beherrscht werden: SIN, COS, TAN
- Stets müssen zwei Werte bekannt sein, um den dritten Wert zu berechnen.
Mit Sin.Cos,Tan zum Ziel
Während man mit der Pythagoras-Funktion lediglich die Längen am rechtwinkligen Dreieck, aber keine Winkel berechnen kann, ist man mit den Trigonometrischen Funktionen Sinus, Cosinus und Tangens in der Lage, fehlende Winkel und natürlich die fehlenden Längen zu berechnen. Man muss sich allerdings im Formelumstellen ein wenig auskennen. Die Kunst besteht darin, das Gesuchte auf die linke Seite zu bekommen.
Zunächst aber sucht man aus den drei Formeln diejenige aus, mit der man die gestellte Aufgabe lösen kann. Dazu ist es nur nötig, dass man sich überlegt, in welcher der drei Grundformeln zwei Werte bekannt sind und auch der gesuchte Wert vorkommt.
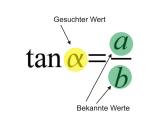
Wenn beispielsweise die Werte von a und b gegeben sind und es soll der Winkel Alpha berechnet werden, dann kommt nur die Tangens-Funktion in Frage, da hier die beiden gegebenen Werte vorkommen.
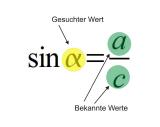
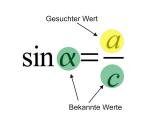
Wenn hingegen die Werte a und c gegeben sind, dann kann der Winkel Alpha nur mit der Sinus-Funktion berechnet werden.
Die Sinus-Funktion wird ebenso verwendet, wenn der Winkel Alpha und die Strecke c gegeben sind und die Länge a berechnet werden soll.
Dies war bereits das ganze Geheimnis der Winkelfunktionen! Entscheidend ist, dass man sich die Grundformel und die Merksätze einprägt und das Formelumstellen übt.
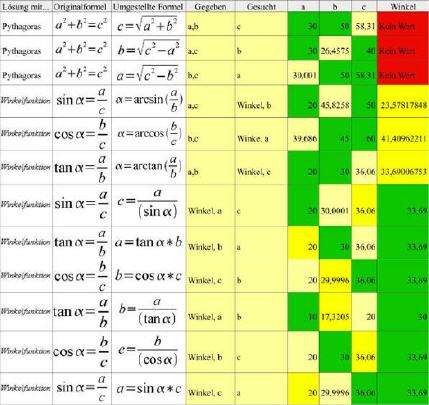
Aber auch wer mit dem Umstellen von Formeln seine Schwierigkeiten hat, soll nicht verzweifeln. In der nachfolgenden Tabelle sind alle Formeln passend zur gesuchten Lösung bereits umgestellt und mit Musterlösungen garniert. Damit hat man dann die Möglichkeit, die Berechnung mit dem Taschenrechner zu üben, da die Musterlösung schon zur Kontrolle gegeben ist. In der Tabelle sind Eingabefelder (bekannte Werte) grün und Ergebnisfelder (gesuchte Werte) in kräftigem Gelb gekennzeichnet.
Nur Übung macht den Meister
Wie die vorherigen Beispiele zeigten, ist es einfach, die trigonometrischen Funktionen anzuwenden. Es ist aber unbedingt notwendig, damit zu üben, um mehr Sicherheit in deren Anwendung zu bekommen. Daher ist es am besten, sich einmal konkrete Aufgaben näher ansehen, die mit den Winkelfunktionen lösbar sind. Aber auch wer sich sehr schwer tut, die Funktionen zu verstehen, der sollte es so machen, wie viele Autofahrer: Zum Autofahren ist es auch nicht nötig, die Funktion eines Verbrennungsmotors zu verstehen. Es genügt, wenn man weiß, wie man schaltet, bremst und die Funktionen der vielen Hebel und Schalter kennt. Jedenfalls ist kein Ingenieursstudium Voraussetzung, um ein Auto zu beherrschen. Mit Formeln sollte ähnlich vorgegangen werden: Diese einfach als Werkzeuge nutzen, selbst wenn man sie noch nicht versteht.
Wie hoch ist ein Baum?
Es ist für das Lernen besonders förderlich, wenn man Beispiele übt, die man selbst gut nachvollziehen kann. Daher werden mit den trigonometrische Funktion zunächst die Höhe von Bäumen berechnet.
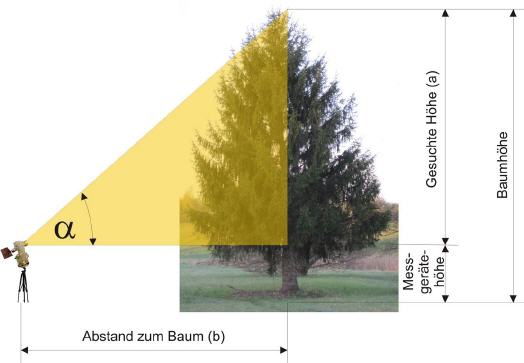
Es genügt, lediglich den Winkel bis zur Baumkrone, sowie den Abstand des Messgerätes vom Baum zu ermitteln. Für die Ermittlung des Winkels muss nicht auf einen teuren Theodoliden zurückgegriffen werden. Ein einfacher, selbst gebastelter Winkelmesser mit einem kleinen Lot an einer Schnur, die in der Mitte des Winkelmesser befestigt ist, würde ähnlich gute Ergebnisse liefern. Es sind aber auch Kompasse verwendbar, wenn diese einen eingebauten Höhenwinkelmesser besitzen.
| Gegeben: | Winkel zum Baumwipfel (Alpha): | 83 Grad |
| Abstand vom Baum zum Messgeräte (b): | 10 Meter | |
| Messgerätehöhe: | 1,7 Meter | |
| Gesucht: | Höhe des Baumabschnittes (a) |
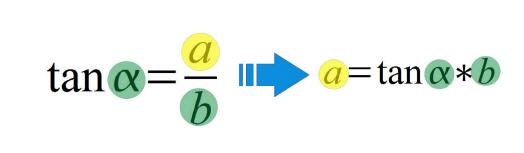
| Berechnung: | a=tan(83)*10 | Ergebnis: 81,44 Meter |
| Um die korrekte Höhe des Baumes zu ermitteln muss zum berechneten Ergebnis lediglich noch die Höhe des Messgerätes vom Boden ermittelt werden. Diese Höhe ist dem Ergebnis der Berechnung zuzuschlagen, was zur Gesamthöhe des Baumes führt. | Baumhöhe=a+Messgerätehöhe | |
| Baumhöhe=81.44+1.70 | Ergebnis: 83.14 Meter |
Die Kunst, Abstände zu berechnen
Trigonometrische Berechnungen werden gerade in Handwerk und Industrie häufig angewendet. Es kommt nicht selten vor, dass die Koordinaten von Bohrungsabstände mit den Winkelfunktionen bestimmt werden müssen, da häufig die Bohrungen lediglich mit einem Radius und mit einem Winkel bemaßt sind.
In der folgenden Aufgabe ist der Winkel und der Abstand von der Scheibenmitte zur Bohrungsmitte gegeben. Für die Berechnung der Koordinaten sind lediglich die Sinus- und die Cosinus-Funktion nötig. Um die Werte a und b berechnen zu können, muss die jeweilige Formel jedoch umgestellt werden.
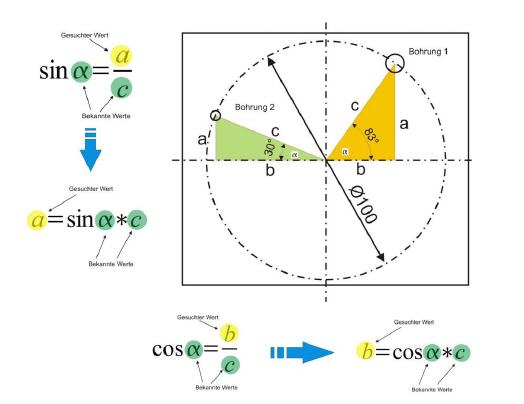
| Gegeben | Teilkreisdurchmesser (c): | 50 Millimeter |
| Winkel (Bohrung 1) : | 83 Grad | |
| Winkel (Bohrung 2): | 30 Grad | |
| Gesucht | Abstand (a) von Bohrung 1 | |
| Abstand (b) von Bohrung 1 | ||
| Abstand (a) von Bohrung 2 | ||
| Abstand (b) von Bohrung 2 |
| Berechnung für Bohrung 1: | a= sin(83) * 50 | Ergebnis: 49.63 mm |
| b= cos (83) * 50 | Ergebnis: 6.09 mm | |
| Berechnung für Bohrung 2: | a= sin(30) * 50 | Ergebnis: 25 mm |
| b= cos(30) * 50 | Ergebnis: 43.3 mm |
Entfernungen leichter schätzen
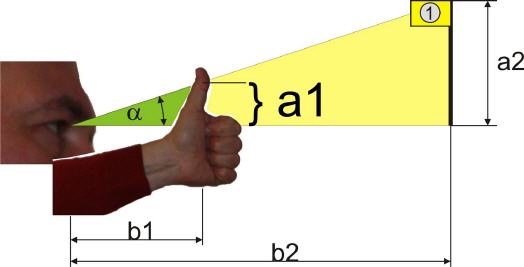
Mit den Winkelfunktionen lassen sich tolle Dinge anstellen. Mit ihnen ist es auch möglich, seinen Daumen zur Entfernungsbestimmung zu benutzen. Dies kann man sich etwa beim Golfspielen zunutze machen, um die Entfernung zum Loch besser abschätzen zu können. Dazu ist es lediglich nötig, die Höhe der Fahnen zu kennen. Die Fahnenhöhe beträgt in der Regel 2,5 Meter. Der Abstand des Daumes zum Auge ist individuell verschieden und muss ermittelt werden.
Nehmen wir an, er beträgt 0,7 Meter. Mit diesen Werte ist es möglich auszurechnen, wie weit die Fahne entfernt ist, wenn diese "am Daumen" 1 cm hoch erscheint. Nämlich 175 Meter. Je näher die Fahne kommt, desto größer wird sie am Daumen erscheinen. Wenn diese am Daumen 3 cm hoch ist, dann beträgt der Abstand zur Fahne nur mehr etwa 58 Meter.
Allerdings funktioniert diese Methode bei Personen, die Maße schlecht schätzen können, nicht so gut. Da gibt es zwei Lösungen: Entweder man zeichnet am Daumen mit einem Filzstift eine Zentimeterskala ein oder man benutzt gleich ein Lineal anstelle des Daumens, um die Entfernung zu bestimmen.
Bleibt nur noch um die verwendete Lösungsformel. Nicht jedem ist sofort klar, wie diese zustande kommt. Nun, dies ist einfach eine Formel, die aus zwei Grundformeln zusammengesetzt wird. Zunächst wird der Winkel aus dem kleinen Dreieck zwischen Auge und Daumen berechnet. Dieser Winkel bildet dann die Grundlage zur endgültigen Berechnung der Entfernung zur Fahne. Diese Entfernung entspricht der Strecke b. Somit wird also anstelle des Winkels einfach die Formel zur Berechnung ebendieses Winkels in die letzte Formel eingefügt.
Um Formeln korrekt umzustellen, ist es wichtig, dass nach dem Umstellen wie bei einer Waage das „Gleichgewicht“ wieder hergestellt ist. Dies bedeutet, dass beim Hinüberziehen einer Funktion diese in ihre „Gegenfunktion“ umgewandelt wird. So wird etwa aus der Wurzelfunktion die Potenzfunktion (und umgekehrt). Auch die Winkelfunktionen müssen umgewandelt werden: Aus Sin wird Arcsin, aus Cos wird Arccos und aus Tan wird Arctan. Dadurch bleibt die Formel nach dem Umstellen im „Gleichgewicht“.
Damit kann nun der Winkel Alpha berechnet werden. Wenn der Winkel bekannt ist, dann kann in einem zweiten Schritt der Abstand zur Golffahne berechnet werden. Mit dem Verschmelzen zweier getrennter Rechenschritte zu einem Einzigen, kann man trigonometrische Berechnungen noch effektiver durchführen.
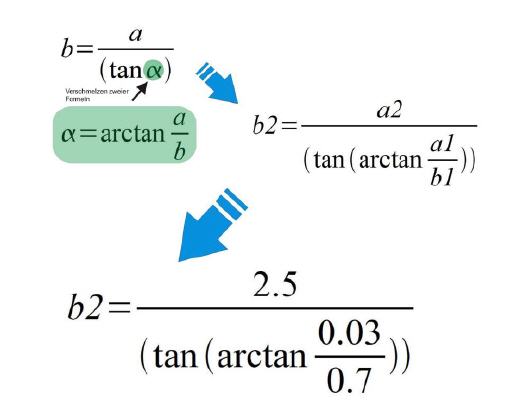
Ergebnis: Abstand vom Standpunkt bis zur Golffahne= 58.31 Meter
Entfernungsmessung mittels Laser
Wenn man etwas Spannung in die Entfernungsbestimmung mittels der Trigonometrie bringen möchte, kann ein einfacher Laserpointer empfohlen werden. Zwei Stück von diesem neumodischen „Zeigegerät“ werden an einem selbstgebastelten Winkelmessgerät befestigt. Dadurch wird es möglich, ebenso einfach wie bei der Berechnung der Baumhöhe, die Entfernung von Häusern, Bäumen et cetera zu ermitteln.
Wichtig ist, dass bei diesen Versuchen der Laserstrahl nicht versehentlich ins Auge gerät, da der Laser die Netzhaut schädigen kann. Laser 2 wird zuerst auf das zu messende Objekt gerichtet. Danach wird der Laserpunkt von Laser 1 mit dem Laserpunkt von Laser 2 in Deckung gebracht und der sich ergebende Winkel abgelesen.
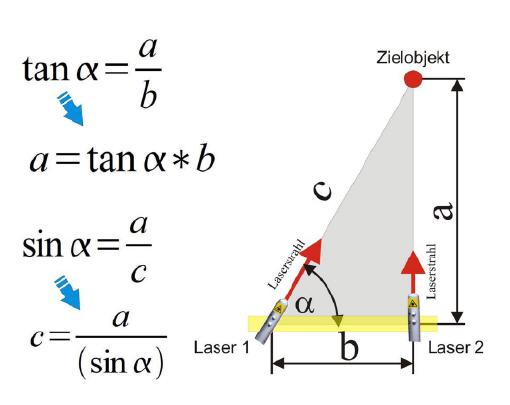
| Gegeben | Abstand zwischen den beiden Laserquellen (b): | 0,7 Meter |
| Winkel zum Zielobjekt: | 86 Grad | |
| Gesucht | Entfernungen a und c |
Um die beiden gesuchten Strecken berechnen zu können, muss schrittweise vorgegangen werden. Zunächst wird Strecke a berechnet, wenn diese bekannt ist, kann Strecke c berechnet werden.
| Berechnung: | a= tan (86) * 0.7 | Ergebnis: a= 10.01 Meter |
| c= 10.01/sin(86) | Ergebnis: c= 10.03 Meter |
Höhe von Wolken ermitteln
Die Meteorologen auf Flughäfen waren immer schon daran interessiert, die Höhe der Wolken zu ermitteln, in der diese ihren Bahnen zogen, um den Flugkapitänen exakte Auskunft für sichere Start- und Landemanöver geben zu können. Hier führte eine ähnliche Idee wie beim Experiment mit dem Laserpointer zum Erfolg. Abgesehen davon, dass es den Laser erst viel später gab, behalfen sich die Meteorologen mit einer starken Lampe, die sie senkrecht in den Himmel richteten. Die Stelle, an der der Lichtstrahl die Wolke traf, trat deutlich hervor. Nun wurde der Winkel zwischen Lampe und reflektierten Lichtstrahl ermittelt, was nach wenig Rechnerei die Wolkenhöhe ergab. Zur Winkelermittlung nutzen die Meteorologen einen sogenannten Pendelquadranten. Es kann jedoch auch unser einfacher Winkelmesser zum Einsatz kommen.
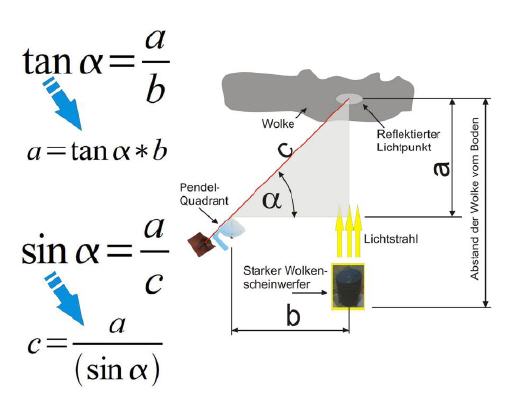
Für die Berechnungen der Wolkenhöhe sind die gleichen Formeln wie für die Laseraufgabe nötig. Der einzige Unterschied ist, dass man, wie im Fall der Baumhöhenmessung, den Abstand vom Boden zum Messgerät noch dazuzählen müsste, um ein korrektes Ergebnis zu bekommen, was aber wohl in diesem Fall nicht notwenig ist.
| Gegeben | Abstand zwischen Wolkenscheinwerfer und Stativ (b): | 50 Meter |
| Winkel zum Zielobjekt: | 89 Grad | |
| Gesucht | Entfernungen a und c |
Um die beiden gesuchten Strecken berechnen zu können, muss schrittweise vorgegangen werden. Zunächst wird Strecke a berechnet, wenn diese bekannt ist, kann Strecke c berechnet werden.
| Berechnung: | a= tan (89) * 50 | Ergebnis: a= 2864.5 Meter |
| c= 2864.5/sin(89) | Ergebnis: c= 2865 Meter |
Bestimmung von Erdumfang und Erddurchmesser
Nachdem durch Üben nun schon tolle Dinge mit den Winkelfunktionen berechnet werden können, soll dieses Wissen zur Berechnung des Erddurchmesser genutzt werden. Dazu sind allerdings wichtige Vorüberlegungen nötig, um dieses Problem überhaupt lösen zu können. Schon 250 v. Christi wusste der Grieche Eratosthenes, wie man solche Probleme pragmatisch angeht. Er beobachtete, dass die Sonne an einem Brunnen in der Stadt Syene, dem heutigen Assuan in Ägypten, keinen Schatten warf. Daraus schloss er, dass die Sonne genau über ihm stand. Ein Jahr später befand er sich in der 800 Kilometer entfernten ägyptischen Hafenstadt Alexandria.
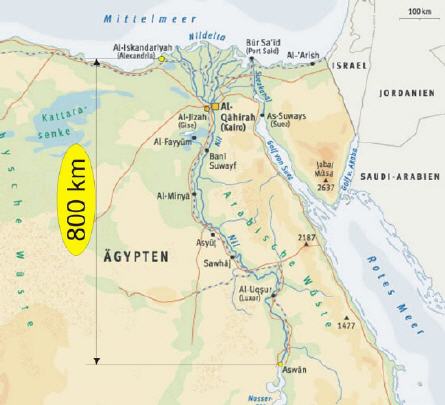
(Bildquelle: Wikipedia)
Am 21.6 maß er die Schattenlänge eines in Alexandria stehenden Obelisken. Aus der Höhe des Obelisken und der Schattenlänge berechnete er den Winkel. Dieser betrug 7,2 Grad. Nachdem er diesen Winkel ermittelt hatte, konnte er den Abstand von der Erdoberfläche zum Erdmittelpunkt berechnen. Eratosthenes wählte dazu den Weg über den Erdumfang.
Er wusste nun, dass 7,2 Grad einer Entfernung von 800 Kilometer auf der Erdkugel entsprachen. Ein Kreis hat bekanntlich einen Winkel von 360 Grad. Er dividierte den Winkel von 7,2 Grad durch 360 und erfuhr, dass 800 km Entfernung der 50te Teil des Erdumfangs ist (360/7,2=50). Also musste er nur die Zahl 50 mit der Entfernung 800 km malnehmen und erhielt so den Erdumfang, der 40.000 km beträgt.
Da sich der Umfang eines Kreise mit dem Kreisdurchmesser mal 3,14 berechnen lässt, muss nur die Formel entsprechend umgestellt werden, um aus dem Kreisumfang den Kreisdurchmesser zu bekommen. Lösung: Kreisumfang dividiert durch 3,14 = 12730 km. Wenn man den Erddurchmesser mit den Winkelfunktionen berechnet, dann fehlen im Ergebnis knapp 65 Kilometer, was daran liegt, dass Eratosthenes den Winkel lediglich mit einer Nachkommastelle messen konnte. Ein Winkel von 7,164 Grad führt nur noch zu einer kleinen Abweichung.
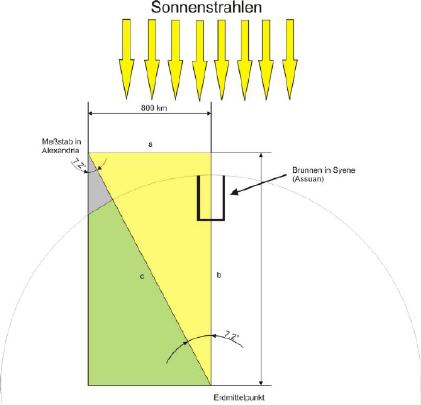
| Berechnung: | b= 800/(tan(7.164) | Ergebnis: b=6.364,81 (dies ist der halbe Erddurchmesser) |
| Erddurchmesser=6364.81*2 | Ergebnis: 12.729,62 km |
Per Zeitmessung zum Monddurchmesser
Eine Mondfinsternis ist die ideale Gelegenheit, um dessen Entfernung und Größe zu berechnen. Aristarch, der von 310 bis 230 v. Chr. lebte, ist dies aufgefallen. Allerdings ist diese Berechnung erst möglich, wenn der Durchmesser der Erde bekannt ist, da es sich bei dieser Berechnung um eine Verhältnisrechnung und keine Rechnung mit Winkelfunktionen handelt. Aber dieses Problem hat ja freundlicherweise Eratosthenes bereits gelöst.
Um den Monddurchmesser zu bestimmen, werden Zeitmessungen durchgeführt. Die Zeitmessung startet, wenn der Mond in den Erdschatten eintritt. In dem Moment, wo er sich komplett im Erdschatten befindet, wird eine Zwischenzeit genommen (tab). Die Zeitmessung wird erst angehalten, wenn der Mond wieder aus dem Erdschatten austritt (tac). Nehmen wir nun folgende Werte an: tab=65 Minuten; tac= 236 Minuten.
Aus dieser Zeitmessung kann man ermitteln, in welchem Verhältnis der Mond kleiner als die Erde ist. Verhältnis=tac/tab. =236/65=3,63. Da der Erddurchmesser bekannt ist, kann der Monddurchmesser leicht berechnet werden. Monddurchmesser=Erddurchmesser / 3,63= 12730/3,63=3506 km. Genaue Messungen ergaben, dass der mittlere Monddurchmesser 3476 km beträgt. Somit ist die Mondfinsternis-Methode recht genau und für eigene Experimente bei der nächsten Mondfinsternis sehr zu empfehlen.
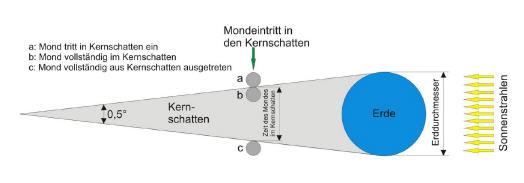
Da nun der Durchmesser des Mondes bekannt ist, kann auch dessen Entfernung bestimmt werden. Hier sind die Winkelfunktionen wieder in ihrem Element, da für die Nutzung der Winkelfunktionen stets zwei bekannte Werte gegeben sein müssen. Dies war ja bei der Bestimmung des Monddurchmessers nicht der Fall. Wir wählen die Tangensfunktion und kommen mit der Berechnung 3500/tan0,5 zum Ergebnis von 401.060 km für die Entfernung Erde-Mond.
| Gegeben | Monddurchmesser (a): | 3476 km |
| Winkel von Mondrand zu Mondrand: | 0,5 Grad | |
| Gesucht | Entfernung Erde-Mond (b) |
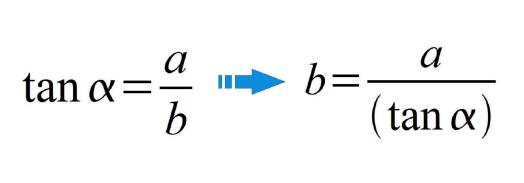
| Berechnung: | b= 3476/(tan(0.5)) | Ergebnis: b=39.8310 km |
Per Winkelfunktion die Mondentfernung berechnen
Da nun der Durchmesser des Mondes bekannt ist, kann auch dessen Entfernung bestimmt werden. Hier sind die Winkelfunktionen wieder in ihrem Element, da für die Nutzung der Winkelfunktionen stets zwei bekannte Werte gegeben sein müssen. Dies war ja bei der Bestimmung des Monddurchmessers nicht der Fall. Wir wählen die Tangensfunktion und kommen mit der Berechnung 3500/tan0,5 zum Ergebnis von 401.060 km für die Entfernung Erde-Mond.
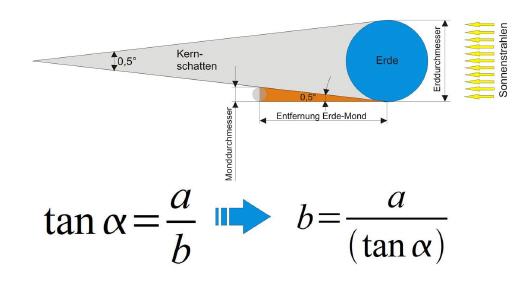
| Gegeben: | Monddurchmesser (a): | 3.476 km |
| Winkel von Mondrand zu Mondrand: | 0,5 Grad | |
| Gesucht: | Entfernung Erde-Mond (b) | |
| Berechnung: | b= 3476/(tan(0.5)) | Ergebnis: b=398.310 km |
Bestimmung der Sonnenentfernung
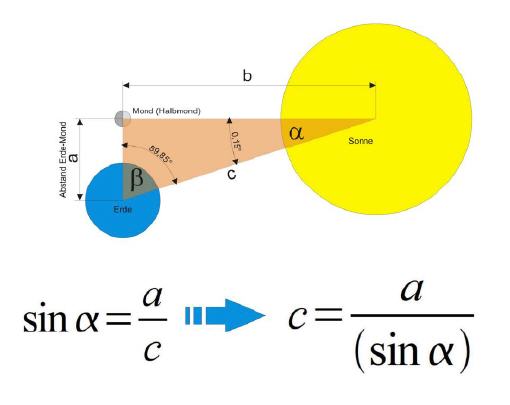
Nachdem nun der Abstand des Mondes zur Erde bekannt ist, kann man folgerichtig auch den Abstand von der Erde zur Sonne berechnen. Dazu ist es nötig, auf Halbmond zu warten. Die Beobachtung beschränkt sich zudem auf Tage, an denen sowohl der Mond, als auch die Sonne am Himmel stehen. Wenn dies der Fall ist, dann kann mit einem geeigneten Winkelmessgerät der Winkel zwischen Mond und Sonne festgelegt werden.
Aristarch hatte natürlich keine so genauen Messgeräte zur Verfügung, die heute den Astronomen zur Verfügung stehen. Daher hat er den Winkel mit 87 Grad ermittelt. Tatsächlich beträgt dieser jedoch 89.85 Grad. Dadurch bekam er lediglich eine Entfernung von rund 7,66 Millionen Kilometer, anstatt 153,17 Millionen Kilometer als Ergebnis. Aber immerhin war nun bekannt, dass die Sonne wesentlich weiter weg war als der Mond.
Hinweis: Das Dreieck ist zum besseren Verständnis übertrieben eingezeichnet.
| Gegeben | Abstand Erde-Mond (a): | 398.000 km |
| Winkel vom Halbmondschatten zur Sonne (Beta): | 89,85 Grad | |
| Gesucht | Winkel Alpha | |
| Sonnenentfernung (c) | ||
| Berechnung: | Winkel= 90-89.85 | Ergebnis: 0,15 Grad |
| c= 398.000/sin(0.15) | Ergebnis: 152.024.975,3 km |
Hinweis: Die offizielle Entfernung zur Sonne beträgt 153,17 Millionen Kilometer
Bestimmung des Sonnendurchmessers
Da ja der Mond und die Sonne sich perfekt überdecken, ist klar, dass auch die Sonne einen Winkel von 0,5 Grad, gemessen von Rand zu Rand, einnimmt. Wenn nun der Sonnenabstand bekannt ist, kann leicht der Sonnendurchmesser ermittelt werden.
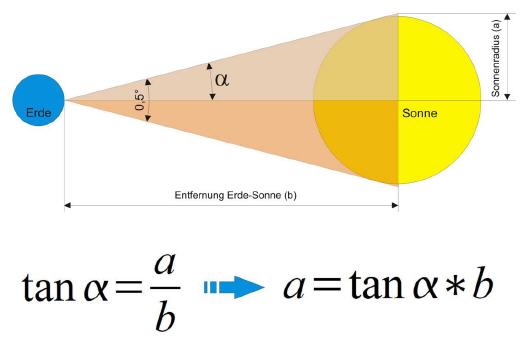
| Gegeben | Entfernung Erde-Sonne (b): | 153 Millionen Kilometer |
| Winkel vom Sonnenrand zum Sonnenrand: | 0,5 Grad | |
| Gesucht | Winkel Alpha | |
| Sonnendurchmesser | ||
| Berechnung: | Winkel Alpha=0.5/2 | Ergebnis: 0,25 Grad |
| Sonnenradius (a) = tan(0,25)*153.000.000 | Ergebnis: 667.592,68 km | |
| Sonnendurchmesser= Sonnenradius*2 | Ergebnis: 1.335.185,35 km |
Der heute bekannte exakte Sonnendurchmesser beträgt 1.391.400 km. Auch hier sieht man, dass schon damals helle Köpfe in der Lage waren, relativ genau unser Planetensystem zu vermessen. Umso unverständlicher, dass es Religionen schafften, das bereits erworbene Wissen wieder verschwinden zu lassen und die These von der Scheibengestalt der Erde, die von der Sonne umkreist wird, durchsetzen konnten.
Derart einfach gestrickte Gestalten in religiösen Kreisen verstummen auch heute noch nicht und versuchen das Rad der Erkenntnis wieder zurückzudrehen. Religiös Verblendete haben jüngst gar einen Zusammenhang zwischen Erdbeben und der Kleidung von Frauen hergestellt. Und das 2300 Jahre nach Aristarch.
Bestimmung weit entfernter Sterne
Mit dem bisher erworbenen Wissen kann nun auch daran gedacht werden, kühne Abstandsberechnung von sehr weit entfernten Sonnensystemen vorzunehmen. Dazu muss man nur den Stern anpeilen und den Winkel Sonne-Stern ermitteln.
Da die Entfernung zur Sonne ja nun bekannt ist, lässt sich so die Entfernung zu einem Stern bestimmen. Dazu ist es der Rechengenauigkeit zuträglich, wenn der Winkel des Sterns jeweils im Abstand eines halben Jahres, etwa am 21.3 und am 23.9, gemessen wird, da dadurch der Winkel genauer ermittelt werden kann. Heutzutage kann man sich den Zeitaufwand sparen, da sowohl im Internet (beispielsweise in Wikipedia) als auch in zahlreichen astronomischen Büchern die Winkel für viele Objekte veröffentlicht sind.
Der Winkel zur roten Riesensonne Aldebaran beträgt 48,94 Millibogensekunden. Um nun die Entfernung zum Stern zu berechnen, müssen zunächst diese Winkelangaben in Dezimalgrad umgewandelt werden. Dazu ist folgende Formel nötig: 48,94/3600/1000.
48,94 Millibogensekunden sind demnach 0.00001359 Grad.
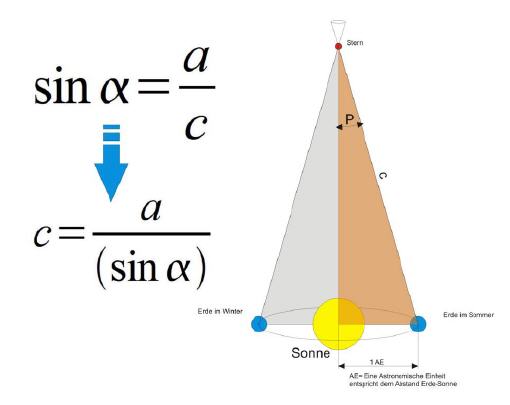
| Gegeben | Abstand Erde-Sonne (a): | 153 Millionen km (= näherungsweise 1 Astronomische Einheit AE) |
| Parallaxenwinkel P von Aldebaran: | 0,00001359 Grad | |
| Gesucht | Abstand Erde-Stern (c) | |
| Umrechnung | 1 AE=149.597.870,691 km | |
| 1 Parsec=206.264,806 AE | ||
| 1 Parsec=3,26 Lichtjahre | ||
| Berechnung: | c= 1/sin(0.00001359) | Ergebnis: 4.214.646,63 AE |
| 4.214.646,63/206.264,806 | Ergebnis: 20,43 Parsec | |
| 20,43*3,26 | Ergebnis: 66,6 Lichtjahre |
Somit ist der Stern Aldebaran 66,6 Lichtjahre von der Erde entfernt.
Download
Diesen Artikel können Sie hier im PDF-Format [3.355 KB]
herunterladen. Eine etwas kürzere Version finden Sie hier [390 KB]
.
Eine Excel-Rechenblattsammlung zu den Winkelfunktionen finden Sie hier [3.446 KB]
. Diese Excel-Datei sollte auch mit anderen Office-Programmen, wie etwa Openoffice, funktionieren. Die Formelblätter sind nicht geschützt und können frei eingesehen und für eigene Zwecke verändert werden. Die Datei darf jedoch nicht als eigenes Werk veröffentlicht werden. In diesem Fall ist stets ein Quellenvermerk "Welt der Fertigung" nötig.
Video
Hier finden Sie ein Video zu den Winkelfunktionen.
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 6 - gesamt: 11068.