Drehmomentermittlung mittels Küchenwaage
Einer wichtigen Maßeinheit auf der Spur
Ein Drehmoment kommt in der Technik sehr häufig zum Vorschein. Damit Maschinenelemente unter der Einwirkung eines Drehmoments nicht zerstört werden, muss deren Dimension zuverlässig ermittelt werden, um sie passend für die auftretende Kraft auszulegen. Zum Verständnis hilft es, einen einfachen Aufbau vorzunehmen, in dem eine Küchenwaage die Hauptrolle spielt.

Die Kraft F ist ein ganz wesentliches Element der Physik. Sie ergibt sich aus der Größe einer Masse sowie deren Beschleunigung und wird in Newton gemessen.
Im Internationalen Einheitensystem wurde festgelegt, dass ein Newton dann gegeben ist, wenn eine Masse m von einem Kilogramm mit 1 m/s2 beschleunigt wird.
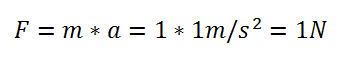
Wenn nun ein Gegenstand mit einem Gewicht von einem Kilogramm auf die Erde fällt, so wird dieser Gegenstand mit 9,81m/s2 beschleunigt.

Dies bedeutet aber auch, dass ruhende Körper ebenfalls mit dieser Konstante in Richtung Erdmittelpunkt gezogen werden. In diesem Fall wird von einer Gewichtskraft gesprochen, die ein Körper auf seinen Untergrund ausübt.

Ein Gewicht von einem Kilogramm besitzt daher folgende Gewichtskraft:
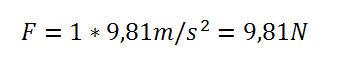
Der Körper übt demnach eine Gewichtskraft von knapp 10 N auf seinen Untergrund aus. Der gleiche Körper würde auf anderen Planeten eine viel größere oder viel kleinere Gewichtskraft auf den Untergrund ausüben, je nachdem, ob dieser Planet größer oder kleiner als die Erde ist.
Übrigens entspricht der Wert von 9,81 N exakt einem Kilopont, der früher gültigen Krafteinheit.
Das Kraftmoment:
Kräfte wirken sehr häufig in Verbindung mit einem Hebel. Dies kann ein Rad, ein Gabelschlüssel oder eine Waage sein. In dem Moment, wo ein Hebel ins Spiel kommt, wird die Kraft verstärkt, zudem wird nun von einem ›Moment‹ gesprochen. Ein Wort, das auch in den Wörtern ›Drehmoment‹, ›Biegemoment‹ und ›Torsionsmoment‹ steckt. Immer dann, wenn von einem Moment die Rede ist, ist eine Kraft gemeint, die an einem (ver)dreh- oder verbiegbaren Körper wirkt.
Je nachdem, wie sich der Körper durch die Krafteinwirkung verhält, wird von folgenden Momenten gesprochen:

Beispiel ›Träger‹:
Wird ein einseitig eingespannter Träger mit einer Länge von zwei Meter mit einer Masse von 25 Kilogramm belastet, so wird das erzeugte Moment wie folgt berechnet:
1. Gewichtskraft berechnen:
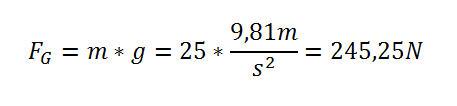
2. Moment berechnen:
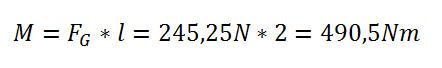
Wie groß nun die Durchbiegung des Trägers durch die Einwirkung dieser Kraft sein wird, hängt von dessen Auslegung ab. Je schwächer die Wandstärke, desto mehr wird dieses Drehmoment den Träger durchbiegen.
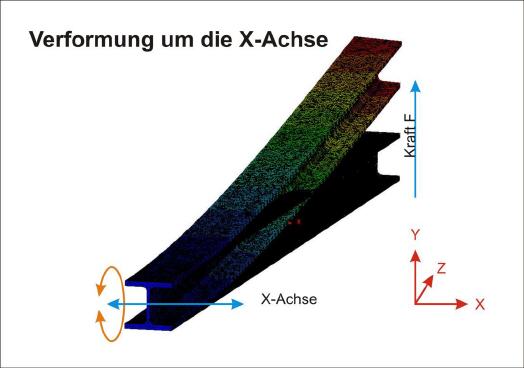
Vertiefung:
Es soll untersucht werden, welches Drehmoment ein Körper von 220 Gramm Gewicht erzeugt, wenn dieser an unterschiedlichen Positionen eines Hebels gehängt wird.

Dazu wird zunächst dessen Gewichtskraft berechnet:
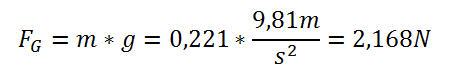
Danach werden die Momente an den unterschiedlichen Positionen berechnet:
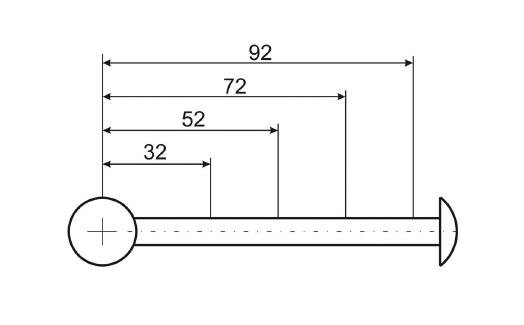
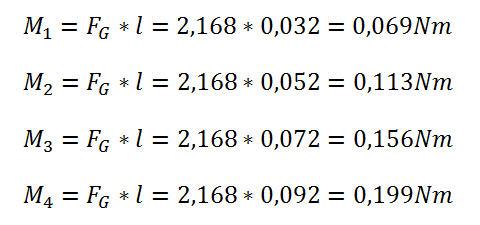
Es zeigt sich, dass das Drehmoment umso größer wird, je weiter außen die Gewichtskraft von 2,168 N wirken kann. Wie ein Diagramm zeigt, erfolgt die Zunahme des Drehmoments linear, wenn das Gewicht stets im gleichen Abstand von 20 Millimeter platziert wird.
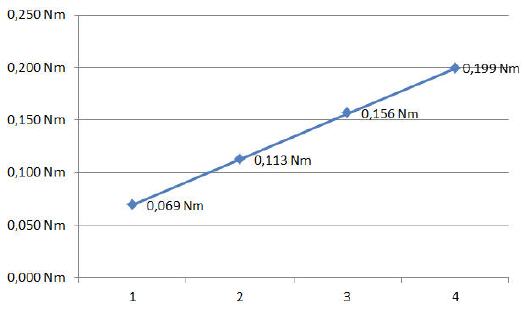
Interessant ist nun festzustellen, ob die berechneten Drehmomentwert sich auch irgendwie bestätigen lassen. Dazu ist eine einfache Küchenwaage hilfreich. Zunächst ist jedoch wichtig zu wissen, dass laut Hebelgesetz sich Kräfte aufheben, wenn sie auf der linken und rechten Seite in gleicher Größe und gleichem Abstand wirken.
Die Formel lautet demnach:
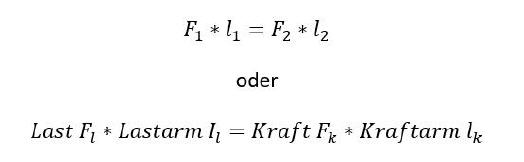
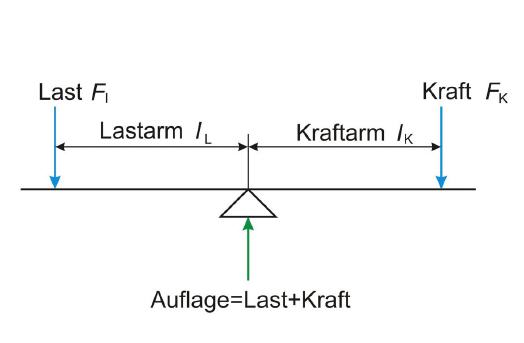
Da es egal ist, ob die Gewichte einer Waage gespiegelt oder um 180 Grad umgelenkt werden, ist eine Küchenwaage nutzbar, um den Wert F1 beziehungsweise die Last Fl zu ermitteln. Dazu muss jedoch eine passende Mechanik aufgebaut und zusätzlich die Waage geeicht werden, schließlich würde das Gewicht der Mechanik die Berechnung verfälschen. Zu diesem Zweck einfach die Mechanik auf die Waage legen und diese danach nullen.

Um Theorie und Praxis überprüfen zu können, wird aus Vereinfachungsgründen zunächst mit gleichen Abständen gerechnet. Dies bedeutet, dass das Gewicht im gleichen Abstand anzubringen ist, den der Auflagepunkt l1 vom Drehpunkt entfernt ist.
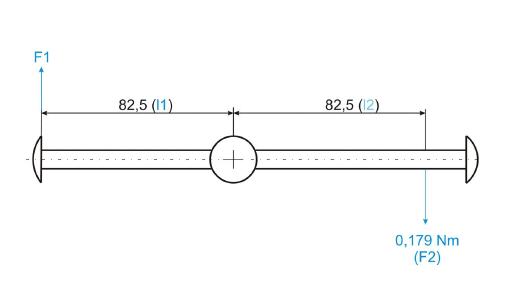
Es muss zunächst die Kraft F1 berechnet werden, die sich ergibt, wenn das Gewicht von 220 Gramm in einem Abstand l2 von 82,5 Millimeter eingehängt wird. Dazu ist die obige Formel umzustellen.
Das Ergebnis der Umstellung lautet:
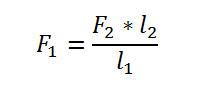
Wenn in die Formel die Daten aus der obigen Zeichnung eingegeben werden, so ergibt sich folgender Wert für F1:
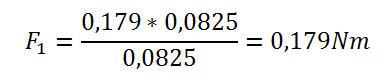
Dies ist ein logisches Resultat, schließlich muss die Berechnung der Kraft F1 den gleichen Wert zum Ergebnis haben, den die Kraft F2 besitzt, da die beiden wirkenden Hebellängen l1 und l2 gleich groß sind.

Die Küchenwaage müsste nun einen Wert anzeigen, der sich aus folgender Formel ergibt:
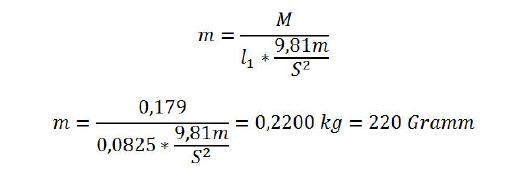
Demnach müsste die Anzeige der Küchenwaage exakt 220 Gramm anzeigen, wenn der Aufbau korrekt vorgenommen wurde und das Gewicht an der korrekten Stelle platziert wurde.

Wie sich zeigt, wurde alles richtig gemacht.
Dieser Rechenweg kann nun genutzt werden, um aus der Gewichtsanzeige der Waage auf das wirkende Moment zu schließen. Alles was dazu nötig ist, ist die Kenntnis der Größe des Gewichts sowie die Länge von l1. Beides ist bekannt: Gewicht m = 220 Gramm, Länge l1 = 82,5 mm.
Nun kann das Gewicht an allen möglichen Längen des Hebels positioniert werden, stets ist es möglich, aus der Anzeige des Gewichts auf das Drehmoment zu schließen.
Die Formel dazu lautet:
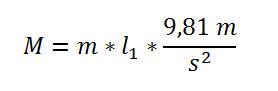
Werden die Werte von vorhin verwendet, so müsste das dort berechnete Drehmoment herauskommen.
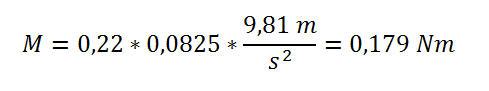
Wie sich zeigt, ist die Berechnung korrekt erfolgt. Nun steht der Berechnung der Drehmomente für unterschiedliche Positionen nichts mehr im Weg. Alles was dazu zusätzlich zum Gewicht m bekannt sein muss, ist der Anzeigenwert der Waage in Gramm sowie die Position des Gewichts in Millimeter.
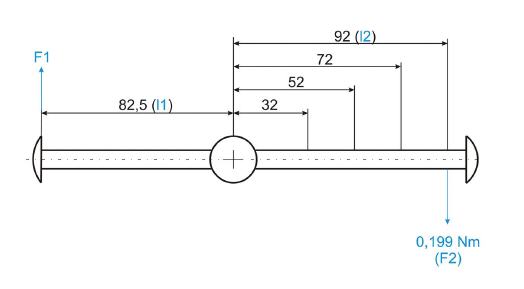
Hier einige Beispiele:
Länge l2=32mm, Waagenanzeige=84 Gramm:
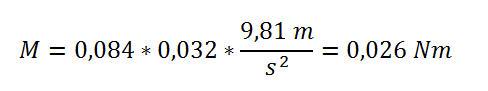
Länge l2 = 52 mm; Waagenanzeige = 136 Gramm; ergibt ein Drehmoment von 0,069 Nm
Länge l2 = 72 mm; Waagenanzeige = 185 Gramm; ergibt ein Drehmoment von 0,131 Nm
Länge l2 = 92 mm; Waagenanzeige = 235 Gramm; ergibt ein Drehmoment von 0,212 Nm
Wie sich zeigt, stimmen die Resultate bis auf kleine Rundungsfehler sehr gut mit den Ergebnissen der am Anfang berechneten Tabelle über die Momente M1 bis M4 überein.
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 5 - gesamt: 11305.















































































