Einführung in Geogebra
Ein staunenswertes Programm für die Technik
Geogebra ist ein erstaunlich leistungsfähiges Softwarepaket, mit dem unter anderem 2D- und 3D-Geometriekörper gezeichnet und animiert werden können. Durch Ziehen von Objekten und Verändern von Parametern ist die Welt der Geometrie anschaulich erlebbar. Mit der Open Source-Software sind Arbeitsblätter erstellbar, mit denen Schüler komplexe Aufgaben auf neue Weise verstehen lernen, weshalb nicht zuletzt Ausbilder einmal einen Blick darauf werfen sollten.
Geogebra hat es bereits weit gebracht. Das leistungsstarke Mathematikprogramm ist in einigen deutschen Bundesländern bereits als Hilfsmittel in der Abiturprüfung zugelassen. Es wurde zum größten Teil von Markus Hohenwarter für seine Diplomarbeit sowie seine Dissertation an der Universität Salzburg entwickelt. Die Software benötigt die Java Runtime Environment und kann sowohl geometrische Konstruktionen als Funktionsgraphen darstellen.
Der Clou ist, dass an beliebiger Stelle auf dem Arbeitsplatz Schieberegler positioniert werden können, mit denen die Größe von Parametern veränderbar ist. Dadurch können sich dynamisch ändernde Körper betrachtet werden. Diese Eigenschaft macht das Programm nicht zuletzt für den Metallbereich interessant, da damit die einwandfreie Funktion von komplizierten mechanischen Bewegungen überprüfbar wird.
Am sinnvollsten ist der Download vom Hersteller des Programms, der die Website www.geogebra.org betreibt. Damit ist sichergestellt, die neueste Version der Software zu erhalten. Das Programm ist für Smartphones, Tablets und natürlich PCs zu haben. Eine ganze Reihe von Betriebssystemen werden unterstützt, sodass wohl für jeden etwas dabei ist.
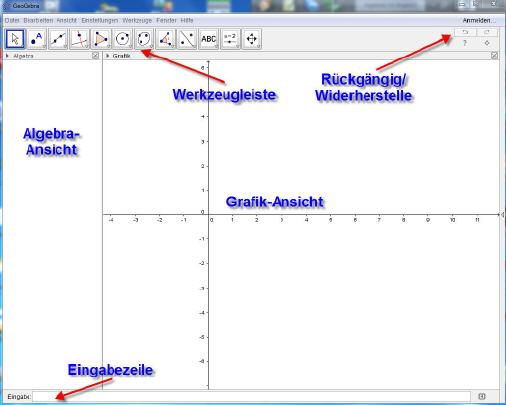
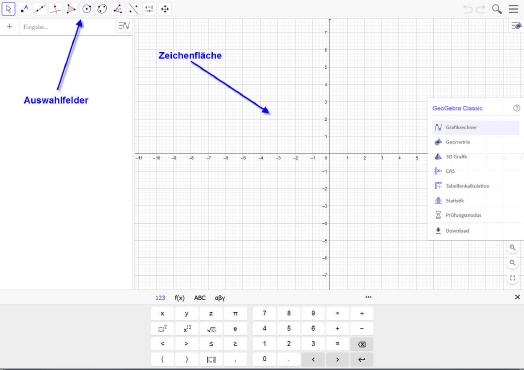
Nachdem die Software installiert und gestartet ist, begrüßt den User ein wohlüberlegt aufgeteilter Bildschirm. Bereits nach kurzer Zeit findet man sich hier zurecht und kann produktiv arbeiten.
Sollten einige Dinge, wie etwa die Eingabezeile nicht angezeigt werden, so müssen diese zunächst im Menü Ansicht/Eigenschaften/Layout aktiviert werden. Dazu genügt es, den Button ›Optionen‹ zu betätigen.
Online-Betrieb:
Es ist nicht zwingend nötig, die umfangreiche Geogebra-Installationsdatei herunterzuladen, da Geogebra auch online genutzt werden kann. Dazu genügt es, www.geogebra.org aufzurufen und danach die gewünschte Anwendung zu starten. Zur Auswahl stehen Classic-Apps und neue Mathe-Apps.
Nach einem Klick auf ›GeoGebra Classic‹ startet Geogebra in derjenigen Version, wie sie oben beschrieben ist. Da Geogebra laufend weiterentwickelt wird, kann es sein, dass das Aussehen des Desktops sich leicht abweichend präsentiert. Die grundsätzliche Bedienung bleibt jedoch bestehen, solange die Entwickler diese nicht ändern. Dazu gibt es keinen Grund, denn die Bedienung ist sehr intuitiv.
Geometrische Figuren zeichnen:
In Geogebra ist es sehr einfach, in die Welt der Geometrie einzutauchen, da sich die nötigen geometrischen Elemente sehr leicht zeichnen und untersuchen lassen.
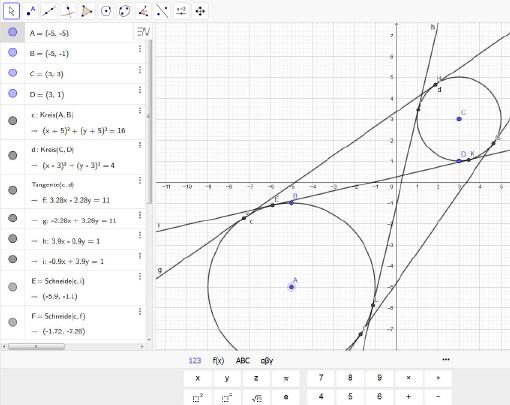
Soll beispielsweise ermittelt werden, auf welche Weise sich Tangenten an zwei Kreisen bilden lassen, so genügt es, zunächst zwei Kreise zu zeichnen und die sich ergebenden Kreise von Geogebra über die Funktion ›Tangenden‹ ermitteln zu lassen. Die dazu nötige Vorgehensweise lautet wie folgt:
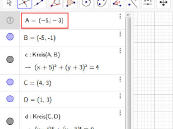
1: Kreise Zeichnen:
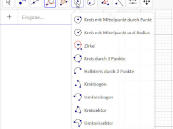
Ein Klick auf das entsprechende Auswahlfeld lässt eine Auswahlliste aufklappen, aus der die passende Funktion ausgewählt werden kann. Der dazugehörende Text ist selbsterklärend, sodass die passende Funktion (Kreis mit Mittelpunkt durch Punkt) sich von selbst findet, um einen Kreis zu zeichnen.
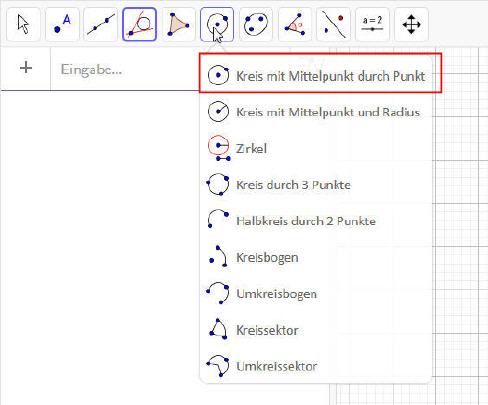
Beim Zeichnen ist das Raster hilfreich, da es eine rastende Funktion hat, sodass sich geometrische Funktionen sehr einfach exakt ausrichten lassen.
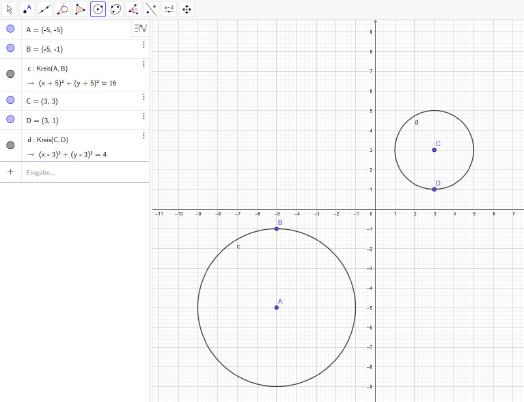
An der linken Seite werden Informationen eingeblendet, die beispielsweise Auskunft geben, an welchen Koordinaten die Kreise gezeichnet wurden.
2. Tangenten erzeugen:
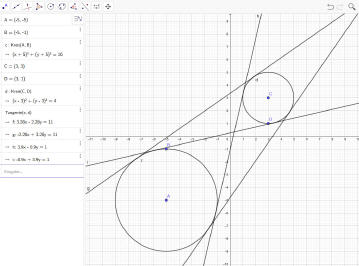
Sollen nun die möglichen Tangenten erzeugt werden, die sich an den beiden Kreisen ergeben, so genügt es, die Funktion ›Tangenten‹ anzuwählen und anschließend die beiden Kreise anzuklicken.
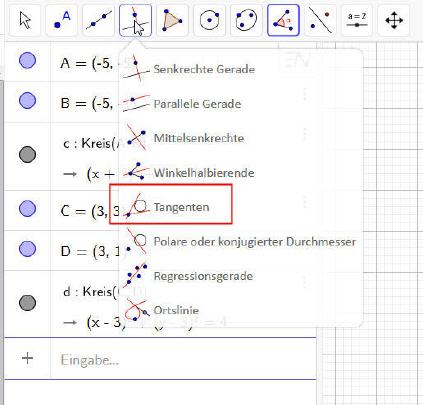
Nachdem Kreise angeklickt wurden, zeichnet Geogebra die sich ergebenden Tangenten ein.
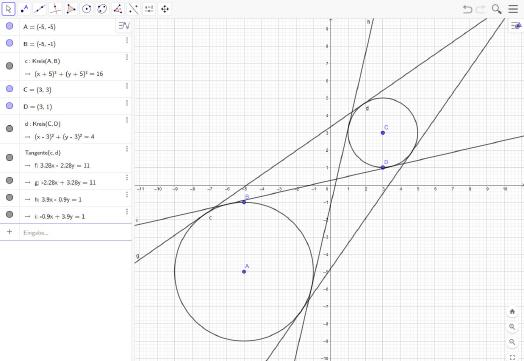
Es sind im Ergebnisfeld allerdings nicht die Berührpunkte mit ihren Koordinaten aufgeführt. Sollen diese ermittelt werden, so müssen diese über die Funktion ›Schneide‹ berechnet werden.
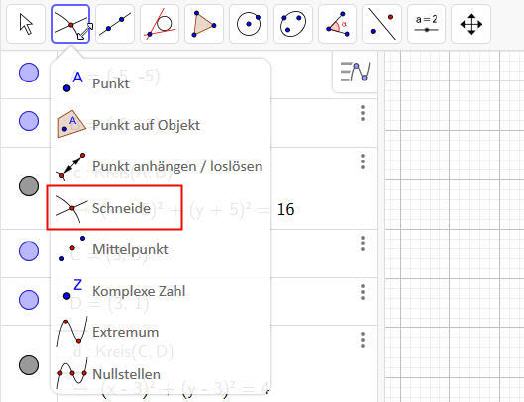
3. Schnittpunkte erzeugen:
Dazu die Funktion aufrufen und diejenigen Elemente anklicken, deren Koordinaten der Schnitt- beziehungsweise Berührpunkte ermittelt werden sollen.
Nachdem alle Punkte ermittelt wurden, können deren Koordinaten im Ergebnisfenster abgelesen werden.
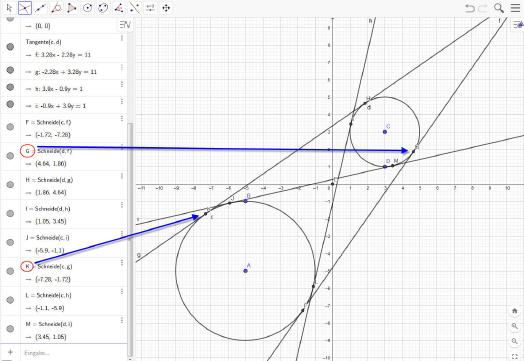
Das eben erstellte Rechenblatt kann nun verwendet werden, um rasch die Koordinaten von Tangenten zu berechnen, die sich an Kreisen mit unterschiedlichsten Durchmessern und Mittelpunktkoordinaten ergeben. Dazu müssen lediglich deren Werte geändert werden.
4. Geometriewerte abändern:
Um die Geometriewerte abändern zu können, genügt es, deren Werte anzuklicken, woraufhin ein Cursor erscheint, mit dessen Hilfe die vorhandenen Werte gelöscht oder ergänzt werden können.
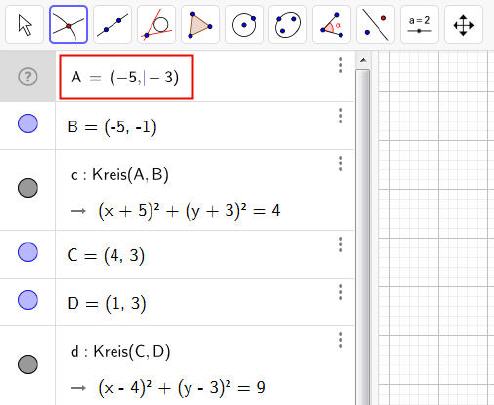
Sofort nach Verlassen des zu ändernden Wertes wird das Element neu berechnet und gezeichnet. Auch die Schnitt- beziehungsweise Tangentenpunkte werden neu berechnet und angezeigt.
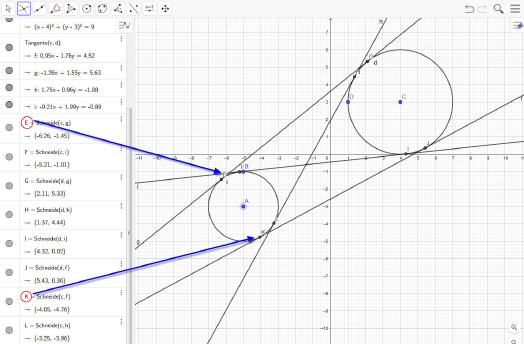
Auf die gleiche Art und Weise können alle anderen Geometrieelemente erzeugt und abgeändert werden.
Stellt das Ergebnis zufrieden, so kann es abgespeichert werden. Obwohl es in der Online-Version zunächst den Anschein hat, dass dies nur in der Cloud möglich wäre, kann die Datei auch auf den eigenen PC gesichert werden. Dazu gibt es zwei Wege: ›Speichern‹ und ›Herunterladen als…‹.
Beide Möglichkeiten lassen sich im rechts obenstehenden Menü-Button auswählen. Egal, welcher Weg gewählt wird – in beiden Fällen wird die Datei im Web-Browser abgelegt und muss von dort in das gewünschte Verzeichnis verschoben werden.
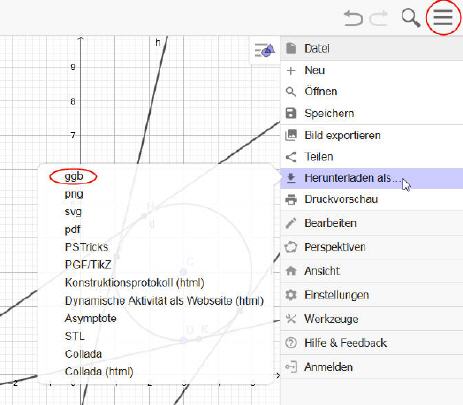
Selbstverständlich ist vor dem Speichern eine individuelle Namensvergabe für die Datei möglich.
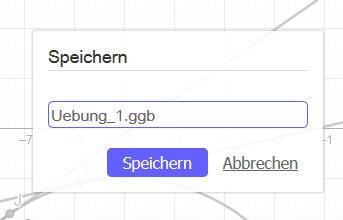
Nach dem Herunterladen von der Geogebra-Seite steht die ggb-Datei im Browser zum Abspeichern in einem Verzeichnis auf dem eigenen PC zur Verfügung.
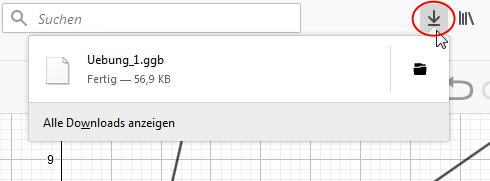
Nach einer erneuten Sitzung mit dem Online-Geogebra-Programm kann die gesicherte ggb-Datei per Drag-and-Drob in die Arbeitsfläche gezogen werden, woraufhin sofort an der selbsterstellten Geogebra-Datei weitergearbeitet werden kann.
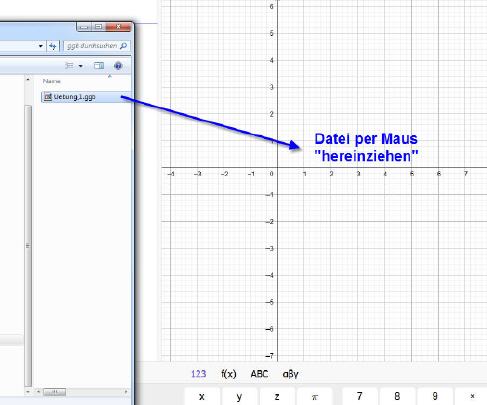
Durch diese Eigenschaft kann man sich eine Installation der Offline-Version von Geogebra in vielen Fällen sparen.
Mehr Informationen:
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 4 - gesamt: 9836.