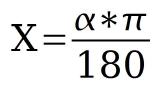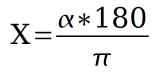@-Funktionen und noch andere CNC-Raffinessen
Nützliche Funktionen für den täglichen CNC-Alltag
In der täglichen CNC-Praxis müssen nicht selten Schnittpunkte berechnet sowie überlange Programme mit raffinierten geometrischen Merkmalen abgearbeitet werden. Der angehende CNC-Fachmann ist also gefordert, die dazu nötigen Funktionen zu kennen und sicher anzuwenden. Deshalb finden sich zum intensiven Üben auch in SIM_WORK der BTR-Betrieb, zahlreiche @-Funktionen sowie ein Geometrierechner, um fit für die reale CNC-Welt zu werden.

Jeder CNC-Programmierer wird immer mal wieder fehlende Schnittpunkte zur Erstellung eines CNC-Programms berechnen müssen. Natürlich sind diese mit den Winkelfunktionen oft rasch errechnet. Mitunter gibt es aber Fälle, die mehr Zeit in Anspruch nehmen, weil diese geometrisch eine Klasse höher als der Durchschnitt liegen. In diesen Fällen können dann CAD-Systeme oder Geometrierechner eingesetzt werden. In SIM_WORK ist so ein Geometrierechner eingebaut, der für viele Zwecke gute Ergebnisse liefert.
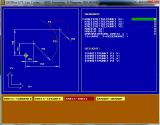
Aus dem Hauptmenü heraus kann dieser Rechner durch Drücken der Tasten [Strg] + [O] aufgerufen werden. Im linken Fenster wird eine Grafische Darstellung der Berechnung angezeigt. Im rechten Fenster können die dazu nötigen Daten eingegeben werden.
Der Rechner ermöglicht es, Schnitt- beziehungsweise Berührpunkte zwischen Gerade-Gerade, Kreis-Kreis,Tangente-Kreis und Sekante-Kreis zu berechnen. Mit den Pfeiltasten [←] und [→] können Sie zwischen den verschieden Berechnungen Hin- und Herwechseln.
Anhand eines Beispiels soll der Umgang mit diesem Rechner erläutert werden. Im Beispiel wird mit einer Zeichnung, die nicht NC-gerecht bemaßt ist, gearbeitet. Es müssen daher einige Maße errechnet werden.
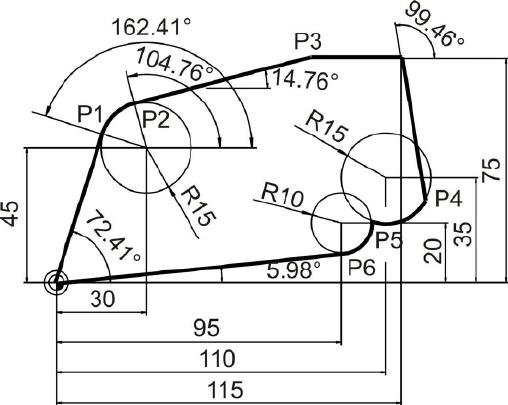
Berechnung des Punktes P1
Bekannt sind: Kreismittelpunkt, Kreisradius, sowie Geradenwinkel. Der Geometrierechner kann mit dem Geradenwinkel nicht direkt rechnen. Er benötigt die Angabe des Tangentenwinkels. Dieser kann durch einfaches Addieren von 90 Grad zum Geradenwinkel leicht errechnet werden.
Daten:
Kreismittelpunkt X: 30
Kreismittelpunkt Y: 45
Radius: 15
Winkel W: 162.41
Ergebnis:
Schnittpunkt P X: 15.7013
Schnittpunkt P Y: 49.5331
Für Punkt P2 muss nur der neue Winkel W 104.76 Grad eingegeben werden, denn alle anderen Daten sind ja noch gültig.
Ergebnis:
Schnittpunkt P X: 26.1784
Schnittpunkt P Y: 59.505
Den Schnittpunkt P3 bilden zwei Gerade. Daher wird per Pfeiltasten [←] oder [→] auf das Feld Gerade-Gerade gewechselt, um den gesuchten Punkt berechnen zu können. Bei beiden Geraden muss der Startpunkt sowie der Geradenwinkel bekannt sein.
Daten:
Startpunkt Gerade X1: 26.1784
Startpunkt Gerade Y1: 59.505
Startpunkt Gerade X2: 115
Startpunkt Gerade Y2: 75
Winkel der Geraden W1: 14.76°
Winkel der Geraden W2: 180°
Ergebnis:
Schnittpunkt X: 84.9908
Schnittpunkt Y: 75
Der Schnittpunkt P4 bildet sich beim Durchdringen einer Geraden durch einen Kreis. Die Gerade bekommt dadurch den Namen "Sekante". Zum Berechnen dieses Punktes wird mit den Pfeiltasten [←] oder [→] zum Feld Kreis-Sekante gewechselt.
Daten:
Startpunkt Gerade X1: 115
Startpunkt Gerade Y1: 75
Winkel der Geraden: 99.46°
Kreismittelpunkt X2: 110
Kreismittelpunkt Y2: 35
Radius R: 15
Als Ergebnis werden zwei Schnittpunkte berechnet. Der Passende muss manuell ausgewählt werden, um zum korrekten Ergebnis zu kommen.
Ergebnis:
Schnittpunkt X1: 122.9315
Schnittpunkt Y1: 27.399
Der Schnittpunkt P5 bildet sich durch Schneiden von zwei Kreisen, daher wird zum Feld Kreis-Kreis gewechselt.
Daten:
Kreismittelpunkt X1: 95
Kreismittelpunkt Y1: 20
Kreismittelpunkt X2: 110
Kreismittelpunkt Y2: 35
Radius R1: 10
Radius R2: 15
Das Ergebnis sind wieder zwei Schnittpunkte, wovon der Passende auszuwählen ist:
Schnittpunkt P X: 104.962
Schnittpunkt P Y: 20.8714
Zum Berechnen von Punkt P6 wird Kreis-Tangente angewählt und die bekannten Werte eingegeben. Es ist zu beachten, dass zum Geradenwinkel, der 5.98 Grad beträgt, 270 Grad dazugezählt werden müssen.
Ergebnis:
Schnittpunkt P X: 96.0418
Schnittpunkt P Y: 10.0544

Überlange Programme
Mit SIM_WORK ist es nicht möglich, Programme mit mehr als 200 Zeilen im Speicher zu bearbeiten. Dabei teilen sich der Hauptprogrammspeicher und der Makrospeicher den Speicherplatz gleichmäßig auf. In beiden Speicherbereichen können je maximal 100 CNC-Programmzeilen untergebracht werden. Auch große Steuerungen stoßen irgendwann an ihre Speichergrenzen. Um dennoch komplizierte und umfangreiche Konturen bearbeiten zu können, bieten viele Steuerungen die Möglichkeit direkt vom PC die NC-Daten entgegenzunehmen. SIM_WORK ist in der Lage, diesen Vorgang zu simulieren.
Zu diesem Zweck müssen aus dem Hauptmenü die Tasten [Strg] + [L] gleichzeitig gleichzeitig betätigt werden. Man befindet sich nun im Laden-Menü.
Wird nun versucht, ein sehr großes Programm in den Speicher zu laden, wird SIM_WORK durch eine Fehlermeldung darauf aufmerksam machen, dass das Programm zu groß ist und der BTR-Betrieb gewählt werden soll.
Mit den Tasten [BILD ↑] oder [BILD ↓] kann zwischen BTR-Betrieb und Textpuffer-Betrieb hin-und hergeschaltet werden. Aktiv ist stets der rot hinterlegte Schalter.
Das Programm Long.txt ist ein überlanges Übungsprogramm. Es kann ganz normal geladen werden. Wenn der BTR-Betrieb richtig angewählt wurde, wird dieses Programm sofort simuliert. Die Simulation würde bei diesem großen Programm jedoch sehr lange dauern. Aus diesem Grund bietet SIM_WORK noch weitere Einstellmöglichkeiten an, um die Simulationszeit zu verkürzen. Dazu sind die Maschinenkonstanten 2 und 3 jeweils auf 1 zu setzen. Dadurch wird zum einen auf die Darstellung der Fräsermittelpunktbahn umgeschaltet und zum anderen die Ablaufgeschwindigkeit der Simulation beträchtlich beschleunigt.
Die @-Funktionen
In SIM_WORK sind über die Grundrechenarten hinaus weitere Rechenfunktionen eingebaut: sogenannten @-Funktionen. @-Funktionen sind nicht im Befehlssatz nach DIN 66025 vorhanden. Sie sind daher nur in ähnlicher Form auf den verschiedenen Industriesteuerungen vorhanden. In SIM_WORK sind folgende Funktionen integriert:
@612 Quadrat
@613 Wurzel
@630 Sinus
@631 Cosinus
@632 Tangens
@634 Arcus Sinus
@635 Arcus Cosinus
@636 Arcus Tangens
@638 Potenz
@640 natürlicher Logarithmus
Das @-Zeichen wird erzeugt, indem die Taste [ALT] gedrückt und dann die Zahl 64 eingegeben wird. Sofort, nachdem die [ALT]-Taste losgelassen wird, erscheint das @-Zeichen am Bildschirm.
Winkelberechnungen können mit diesen Funktionen nur im Bogenmaß durchgeführt werden. Dazu müssen die Winkel umgerechnet werden:
Umwandlung von Grad in Bogenmaß
Umwandlung von Bogenmaß in Grad
Mit den @-Funktionen sind recht interessante Lösungen möglich, um komplizierte Konturen, die sich relativ einfach mathematisch beschreiben lassen, ohne CAM-System zu erstellen.
Die Epizykloide
Eine Epizykloide beschreibt ein fester Punkt am Umfang eines Kreises, wenn sich dieser Kreis, ohne zu gleiten, auf der Außenseite eines festen Kreises abrollt. Die Formeln dafür lauten:
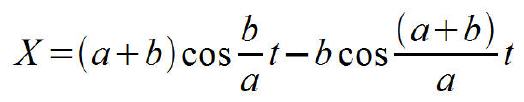
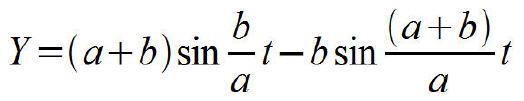
Erläuterung zu den Formelzeichen:
a Radius des festen Kreises
b Radius des rollenden Kreise
t Wälzwinkel
%PM |
N602 @631 (Cosinus) |
Die Hypozykloide
Eine Hypozykloide beschreibt ein fester Punkt am Umfang eines Kreises, wenn sich dieser Kreis, ohne zu gleiten, auf der Innenseite eines festen Kreises abrollt. Die Formeln lauten:
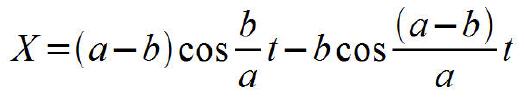
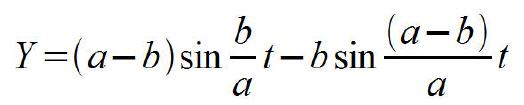
Erläuterung zu den Formelzeichen:
a Radius des festen Kreises
b Radius des rollenden Kreises
t Wälzwinkel
Da diese Formeln, den Formeln zur Berechnung der Epizykloide ähneln, muss das Programm nur ein wenig umgeschrieben werden.
%PM |
N610 E23=E99 (Ergebnis sichern) |
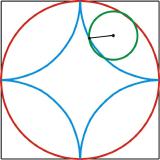
Die Kardioide
Eine Kardioide ist eine Abwandlung der Epizykloide. Die typische Herzform entsteht, wenn ein Kreis auf einem gleichgroßen Kreis abrollt. Da das Programm eine Abwandlung des bereits bekannten Epizykloiden-Programms ist, werden nur mehr ein Ausschnitt dargestellt dargestellt und die Unterschiede gefettet hervorgehoben.
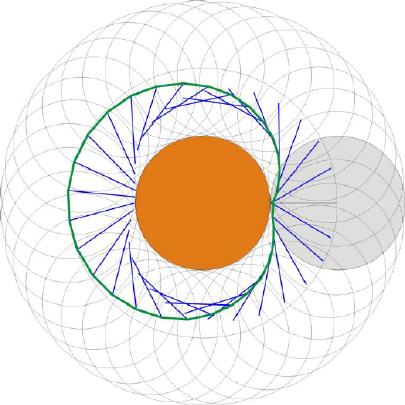
Kardioide
%PM |
N470 E61=40 (Radius rollender Kreis b) |
Download
Diesen Kursteil können Sie hier als PDF-Datei [1.488 KB]
herunterladen.
Die dazugehörenden Programme finden Sie hier als selbstentpackende 7-ZIP-Datei [143 KB]
.
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 3 - gesamt: 19522.