Neue Rechenfunktionen für ergraute CNC-Oldies
Alte Steuerungen zu mehr Leistung führen
Zahlreiche Unternehmen besitzen noch Maschinen, an denen zwar CNC-Bahnsteuerungen angebaut sind, die jedoch keine Möglichkeit bieten, Winkelfunktionen im CNC-Programm zu verwenden. Vielfach können diese Oldies, wie eben die Philips 432, für anspruchsvolle Aufgaben herangezogen werden, da ein Geometrierechner eingebaut ist. Dieser ist jedoch nur schwer handhabbar. Mit etwas Investition in Zeit sind diese Steuerungen schnell in der Lage, mit trigonometrischen Funktionen umzugehen, um so auf einfache Weise anspruchsvolle Werkstücke zu bearbeiten.

Frästeil, erstellt mit Winkelfunktionen
Trigonometrische Funktionen, auch Winkelfunktionen genannt, können aus den vier Grundrechenarten leicht selbst programmiert werden. Dazu ist lediglich ein Blick in eine Formelsammlung nötig, um zu ergründen, wie diese Funktionen aufgebaut sind. In einer solchen Formelsammlung wird ersichtlich, dass trigonometrische Funktionen durch sogenannte „Trigonometrische Reihen“ gebildet werden.
Wenn CNC-Steuerungen die trigonometrischen Funktionen beherrschen, können beispielsweise bestimmte Größen am rechtwinkligen Dreieck, wie etwa der Winkel Alpha oder die Länge von An- und Gegenkathete, problemlos berechnet werden, was das Programmieren komplizierter Konturen sehr erleichtert und die CNC-Programme stark verkürzt.
Natürlich stellt sich die Frage, welchen Sinn es macht, derartige Überlegungen anzustellen, da Steuerungen im Bedarfsfall von CAM-Systemen gefüttert werden. Wer jedoch als CNC-Programmierer alle Tricks kennt, wird sehr oft darauf verzichten können und kommt dennoch schnell ans Ziel.
Sinnvollerweise werde die Erweiterungsprogramme für Steuerungen ohne Winkelfunktionen als Makros im Unterprogrammspeicher abgelegt. Danach können sie von einem beliebigen Hauptprogramm angesprochen und verwendet werden.

Philips 432-Bahnsteuerung
CNC-Oldies kann per Makro-Programmen zu neuen Funktions-Höhenflügen verholfen werden.
Mit Makros zum Ziel
Die Handhabung von selbstprogrammierten Funktionen ist immer ähnlich: Die zu berechnenden Werte werden im Parameterspeicher abgelegt und danach die gewünschte Rechenfunktion durch das entsprechende Makro aufgerufen. Auch das Makro verwendet den Parameterspeicher, um Zwischenergebnisse festzuhalten. Nachdem das Makro abgearbeitet wurde, können wiederum aus dem Parameterspeicher die Ergebniswerte ausgelesen werden.
Der Sinus
Allen Reihen ist gemeinsam, dass die Ergebnisse umso genauer werden, je länger die Reihe ist. Zum Verständnis soll hier das Prinzip vorgestellt werden, damit jeder, der eine höhere Rechengenauigkeit benötigt, ganz einfach das jeweilige Makro ergänzen und ausbauen kann.
Wie an der Formel zur Berechnung des Sinuswertes sichtbar wird, sind die Fakultät und die Potenzfunktion nötig, um den Sinus zu berechnen. Wichtig ist, dass der Winkel des Dreiecks von Grad in Bogenmaß umgerechnet wird, da sonst der Sinus falsch berechnet wird. In der Umwandlungsformel von Grad nach Bogenmaß steht das griechische Zeichen Alpha (α für den Winkel zwischen Ankathete und Hypotenuse und das Zeichen Pi (π) ist die Abkürzung für den Zahlenwert 3,141592654. Wenn beispielsweise ein Winkel von 30 Grad gegeben ist, dann ist durch Umrechnen in das Bogenmaß der Wert 0.5233333 das Ergebnis.
Dieser Wert ist schon recht nahe am korrekten Sinus, der für einen Winkel von 30 Grad exakt 0.5 beträgt. Durch abwechselndes Subtrahieren und Addieren der Ergebnisse aus der Division von Potenzwert und Fakultät wird das Ergebnis in Sinusform schrittweise verfeinert, bis nach einer endlichen Anzahl von Rechenschritten das Ergebnis für den Zweck hinreichend genau erscheint. In der Regel reichen dafür drei Wiederholungen, wie das Schema in Abbildung 1 zeigt.
Wem die Genauigkeit durch drei Iterationen nicht ausreicht, der kann auf ganz einfache Weise selbst die Formel für den Sinus erweitern. Es sind lediglich folgende Merkmale zu beachten, um die Formel fehlerfrei und funktionsfähig zu erweitern:
- Potenz und Faktor müssen für jeden neuen Rechenschritt um die Zahl 2 erhöht werden.
- Die Formel beginnt mit MINUS (X-) und wechselt sind nach jedem Rechenschritt mit PLUS ab.
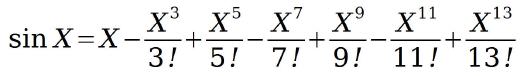
Abb.3 Erweiterung der Sinusfunktion
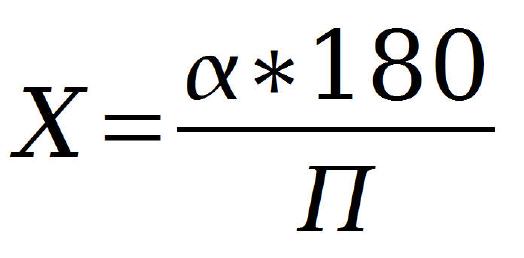
Abb. 4 Umrechnung Bogenmass in Grad
In Abbildung 3 ist ersichtlich, wie die Erweiterung der Sinusformel zu Erhöhung der Rechengenauigkeit auszusehen hat. Es ist leicht erkennbar, dass der Wechsel von MINUS und PLUS einer Sinusform entspricht und dazu führt, dass das Rechenergebnis schrittweise verfeinert und angenähert wird.
Wer das genannte Prinzip beachtet, kann die Formel endlos verlängern und natürlich die Rechenzeit entsprechend in die Höhe treiben. Es ist sinnvoll, den Rechenaufwand zu begrenzen, da sehr rasch kleinste Werte erreicht werden, die nicht mehr entscheidend zu einer wesentlich höheren Rechengenauigkeit beitragen.
Darüber hinaus kann es sogar passieren, dass man sich vom korrekten Rechenergebnis entfernt, was durch Rundungsfehler sehr schnell passiert. Zudem kann es passieren, dass der Speicher überläuft und SIM_WORK abstürzt. In der Regel sollten jedoch etwa 24 Iterationen kein Problem darstellen. Mehr als 14 Iterationen werden jedoch selten nötig sein, um eine ausreichend hohe Rechengenauigkeit zu erzielen.
Wenn das Ergebnis vorliegt, dann muss dieses natürlich wieder vom Bogenmaß in Grad umgerechnet werden. Man benutze dazu die Formel nach Abbildung 4.
Frisch ans Werk
Damit wäre das Rüstzeug vorhanden, um daran zu gehen, das Wissen in CNC-Code zu gießen. Es werden vier Unterprogramme benötigt, die Potenz, Fakultät, Bogenmaß und Grad berechnen. Diese Unterprogramme werden von einem Hauptprogramm aufgerufen. Diese sinnvolle Aufteilung hat den Vorteil, dass auch andere Hauptprogramme auf die jeweiligen Unterprogramme zugreifen können.
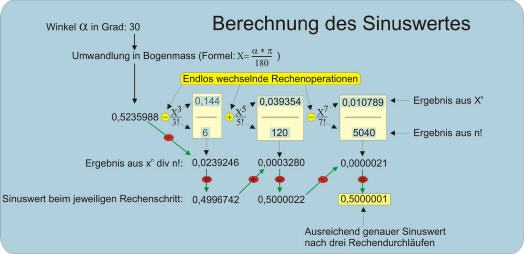
Abb. 5: Berechnung des Sinus eines Winkels
Wichtige Regeln
Wer mit Unterprogrammen und Parametern arbeitet, sollte sich eine Liste erstellen, in die er einträgt, welche Parameter für was für Funktionen verwendet werden. So kann man beispielsweise festlegen, dass die Parameter E80 bis E95 ausschließlich für die laufenden Berechnungen verwendet werden, der Parameter E70 stets für den Winkel reserviert ist und der Parameter E99 immer für die Ergebnisausgabe verwendet wird. Dies sind jedoch unverbindliche Vorschläge, die problemlos abzuwandeln sind.
Die Philips-432-CNC-Steuerung verwendet für Parameter den Buchstaben "E". Natürlich ist klar, dass die Steuerungen anderer Hersteller andere Buchstaben als “E” für Parameter verwenden. Diesbezüglich also unbedingt die jeweiligen CNC-Befehlshandbücher der eigenen Steuerung beachten.
Es bietet sich an, Parameter, die nur lokal in einem Unterprogramm verwendet werden, explizit dort mit einem erklärenden Kommentar zu benennen, um selbst noch nach Jahren die Funktion des Unterprogramms nachvollziehen zu können. Dadurch wird es selbst für einen Kollegen, der nicht in diese Arbeiten involviert war, ein Leichtes, Erweiterungen vorzunehmen.
Wichtige CNC-Makros
%MM
N222222 (Grad in Bogenmass)
N10 E70=E70*3.141592654
N20 E70=E70/180
N333333 (Bogenmass in Grad)
N10 E70=E70*180
N20 E70=E70/3.141592654
N444444 (Potenz)
N10 (E70=Winkel in Bogenmass bzw. Sinuswert)
N20 (E81=Potenzwert)
N30 (E82=Rechenvariable)
N40 (E99=Ergebnis)
N45 E81=E81-2 (Schleifendurchlauf reduzieren)
N50 E82=E70 (Nennwert in Rechenvariable uebergeben)
N60 E82=E82*E70 (Potenzberechnung)
N70 G14 N1=60 N2=60 J=E81 (Schleife)
N80 E99=E82 (Ergebnis)
N555555 (Fakultaet)
N10 (E81=Fakultaetswert)
N20 (E99=Ergebnis)
N30 E81=E81-1 (Schleifendurchlauf um 1 reduzieren)
N50 E82=1 (Multiplikator)
N60 E83=1 (Startwert)
N70 E83=E83*E82 (Fakultaet berechnen)
N80 E82=E82+1 (Multiplikator um 1 erhoehen)
N90 G14 N1=70 N2=80 J=E81
N100 E99=E83 (Ergebnis)
Sinusfunktion als CNC-Programm
%MM
N666666 (Sinus)
N10 (70=Winkel in Grad)
N12 (E40=Potenzwert)
N20 (E41=Ergebnis Potenzberechnung 3)
N21 (E42=Ergebnis Potenzberechnung 5)
N22 (E43=Ergebnis Potenzberechnung 7)
N25 (E51=Ergebnis Fakultaet 3!)
N30 (E52=Ergebnis Fakultaet 5!)
N32 (E53=Ergebnis Fakultaet 7!)
N40 (E87=Ergebnis Potenz div Fakultaet)
N50 (E88=Angenaeherter Sinuswert nach Rechenschritt n)
N55 (E93= Ergebnis Sinus fest gespeichert)
N60 (E99=Ergebnise)
N62 (*** Winkel von Grad in Bogenmass umrechnen ***)
N63 E70=E70*3.141592654
N64 E70=E70/180
N70 (*** Potenz berechnen ***)
N71 E40=3
N71 E40=E40-2 (Schleifendurchlauf reduzieren)
N72 E41=E70 (Nennwert in Rechenvariable uebergeben)
N73 E41=E41*E70 (Potenzberechnung)
N74 G14 N1=73 N2=73 J=E40 (Schleife)
N75 E40=5
N76 E40=E40-2 (Schleifendurchlauf reduzieren)
N77 E42=E70 (Nennwert in Rechenvariable uebergeben)
N78 E42=E42*E70 (Potenzberechnung)
N79 G14 N1=78 N2=78 J=E40 (Schleife)
N80 E40=7
N81 E40=E40-2 (Schleifendurchlauf reduzieren)
N82 E43=E70 (Nennwert in Rechenvariable uebergeben)
N83 E43=E43*E70 (Potenzberechnung)
N84 G14 N1=83 N2=83 J=E40 (Schleife)
N85 (*** Ende Potenz berechnen ***)
N90 (*** Fakultaet zuweisen ***)
N91 E51=6 (Fakultaet 3!)
N92 E52=120 (Fakultaet 5!)
N93 E53=5040 (Fakultaet 7!)
N95 (*** Ende Fakultaet ***)
N97 (*** Erster Rechenschritt ***)
N100 E87=E41/E51 (Ergebnis 1)
N110 E88=E70-E87 (MINUS)
N120 (*** Zweiter Rechenschritt ***)
N130 E87=E42/E52 (Ergebnis 2)
N140 E88=E88+E87 (PLUS)
N150 (*** Dritter Rechenschritt ***)
N160 E87=E43/E53 (Ergebnis 3)
N170 E88=E88-E87 (MINUS)
N175 E93=E88 (Sinus fest speichern)
N180 E99=E88 (Ergebnis Sinus)
Cosinus
Wie an der Sinusfunktion sichtbar wurde, ist es nicht besonders schwer, trigonometrische Funktionen zu verstehen und mittels CNC-Befehlen nachzubauen. Ebenso wie die Sinusfunktion, ist die Cosinusfunktion leicht zu durchschauen. Auch beim Cosinus wird mit Potenzen und der Fakultät gearbeitet, um zum korrekten Ergebnis zu kommen.
Selbstverständlich muss auch hier, wie generell beim Rechnen mit Winkelfunktionen, der Winkel zunächst von Grad in Bogenmaß umgerechnet werden, um die Formel verwenden zu können. Auch diese Formel kann natürlich erweitert werden, wenn eine größere Rechengenauigkeit gewünscht wird. Die Formeln in den Abbildungen 4 und 5 zeigen, wie es gemacht wird.
Das CNC-Programm zum Berechnen des Cosinus eines Winkels ist sinnvollerweise wieder als Unterprogramm zu schreiben, damit es von allen Hauptprogrammen aus aufgerufen werden kann und so universell einsetzbar ist. Generell sollte man sich angewöhnen, alle CNC-Programme, die öfters benötigt werden, als Unterprogramme auszuführen, damit das Hauptprogramm kompakt und übersichtlich bleibt und darüber hinaus geprüfter CNC-Code zum Einsatz kommt.
Cosinusfunktion als CNC-Programm
%MM
N777777 (Cosinus)
N10 (70=Winkel in Grad)
N12 (E40=Potenzwert)
N20 (E41=Ergebnis Potenzberechnung 2)
N21 (E42=Ergebnis Potenzberechnung 4)
N22 (E43=Ergebnis Potenzberechnung 6)
N25 (E51=Ergebnis Fakultaet 2!)
N30 (E52=Ergebnis Fakultaet 4!)
N32 (E53=Ergebnis Fakultaet 6!)
N34 (E60 bis E66=Berechnungszwischenspeicher)
N44 (E87=Ergebnis Potenz div Fakultaet)
N55 (E94= Ergebnis Cosinus fest gespeichert)
N60 (E99=Ergebnis des Cosinuswertes)
N62 (*** Winkel von Grad in Bogenmass umrechnen ***)
N63 E70=E70*3.141592654
N64 E70=E70/180
N70 (*** Potenz berechnen ***)
N71 E40=2
N71 E40=E40-2 (Schleifendurchlauf reduzieren)
N72 E41=E70 (Nennwert in Rechenvariable uebergeben)
N73 E41=E41*E70 (Potenzberechnung)
N74 G14 N1=73 N2=73 J=E40 (Schleife)
N75 E40=4
N76 E40=E40-2 (Schleifendurchlauf reduzieren)
N77 E42=E70 (Nennwert in Rechenvariable uebergeben)
N78 E42=E42*E70 (Potenzberechnung)
N79 G14 N1=78 N2=78 J=E40 (Schleife)
N80 E40=6
N81 E40=E40-2 (Schleifendurchlauf reduzieren)
N82 E43=E70 (Nennwert in Rechenvariable uebergeben)
N83 E43=E43*E70 (Potenzberechnung)
N84 G14 N1=83 N2=83 J=E40 (Schleife)
N85 (*** Ende Potenz berechnen ***)
N90 (*** Fakultaet zuweisen ***)
N91 E51=2 (Fakultaet 2!)
N92 E52=24 (Fakultaet 4!)
N93 E53=720 (Fakultaet 6!)
N95 (*** Ende Fakultaet ***)
N97 (*** Erster Rechenschritt ***)
N100 E60=E41/E51 (Ergebnis 1)
N105 E66=1
N110 E61=E66-E60 (MINUS)
N120 (*** Zweiter Rechenschritt ***)
N130 E62=E42/E52 (Ergebnis 2)
N140 E63=E61+E62 (PLUS)
N150 (*** Dritter Rechenschritt ***)
N160 E64=E43/E53 (Ergebnis 3)
N170 E65=E63-E64 (MINUS)
N172 E94=E65 (Cosinus fest gespeichert)
N180 E99=E65 (Ergebnis Cosinus)
Tangens
Die Berechnung des Tangens ist ebenfalls nicht besonders schwierig. Auch in diesem Fall findet sich die Formel dafür in einer gut sortierten Formelsammlung. Abbildung 6 zeigt die Reihe für die Berechnung des Tangens. Wie bei den anderen trigonometrischen Formeln kann auch diese Reihe endlos fortgeschrieben werden.
Der Tangens ist praktischerweise noch auf ganz andere Weise zu berechnen. Die Regel, dass mehrere Wege ans Ziel respektive nach Rom führen, gilt auch in der Mathematik. Besonders schön ist es, wenn der alternative Weg auch noch kürzer und genauer ist. Dazu benötigt man den Sinus des Winkels und teilt diesen durch den Cosinus des Winkels. Die Formel dazu findet sich in Abbildung 7. Die Anwendung dieser Formel hat den Vorteil, dass das CNC-Programm zur Tangensberechnung wesentlich kürzer ausfällt, was der Lesbarkeit besonders zugutekommt und zudem Programmierfehler stark vermindert werden.

Abb.6 Berechnung des Tangenswertes
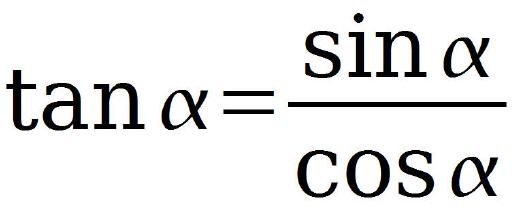
Abb.7 Berechnung des Tangens
Tangens (Variante 1)
%MM
N888888 (Tangens Variante 1)
N10 (70=Winkel in Grad)
N12 (E40=Potenzwert)
N20 (E41=Ergebnis Potenzberechnung 3)
N21 (E42=Ergebnis Potenzberechnung 5)
N22 (E43=Ergebnis Potenzberechnung 7)
N20 (E85=Ergebnis Potenzberechnung)
N50 (E88=Angenaeherter Tangenswert nach Rechenschritt n)
N55 (E93= Ergebnis Sinus fest gespeichert)
N56 (E94= Ergebnis Cosinus fest gespeichert)
N60 (E99=Ergebnis des Tangenswertes)
N62 (*** Winkel von Grad in Bogenmass umrechnen ***)
N63 E70=E70*3.141592654
N64 E70=E70/180
N70 (*** Potenz berechnen ***)
N71 E40=3
N71 E40=E40-2 (Schleifendurchlauf reduzieren)
N72 E41=E70 (Nennwert in Rechenvariable uebergeben)
N73 E41=E41*E70 (Potenzberechnung)
N74 G14 N1=73 N2=73 J=E40 (Schleife)
N75 E40=5
N76 E40=E40-2 (Schleifendurchlauf reduzieren)
N77 E42=E70 (Nennwert in Rechenvariable uebergeben)
N78 E42=E42*E70 (Potenzberechnung)
N79 G14 N1=78 N2=78 J=E40 (Schleife)
N80 E40=7
N81 E40=E40-2 (Schleifendurchlauf reduzieren)
N82 E43=E70 (Nennwert in Rechenvariable uebergeben)
N83 E43=E43*E70 (Potenzberechnung)
N84 G14 N1=83 N2=83 J=E40 (Schleife)
N85 (*** Ende Potenz berechnen ***)
N87 (*** Erster Rechenschritt ***)
N90 E60=1/3
N150 E88=E60*E41 (Tangens nach Schritt 1)
N155 (*** Zweiter Rechenschritt ***)
N180 E61=2/15
N182 E62=E61*E42
N230 E88=E88+E62 (Tangens nach Schritt 2)
N260 E63=17/315
N262 E64=E63*E43
N270 E88=E88+E64 (Tangens nach Schritt 3)
N280 E99=E88 (Ergebnis Tangens)
Tangens (Variante 2)
N999999 (Tangens Variante 2)
N10 E99=E93/E94 (Sinus div Cosinus = Tangens)
N20 E95=E99 (Tangens fest gespeichert)
Umkehrfunktionen
Die Behandlung der trigonometrischen Funktionen wäre unvollständig, wenn nicht auch die jeweiligen Umkehrfunktionen erläutert werden, mit denen aus den berechneten Werten wieder ein Winkel bestimmt werden könnte. Daher folgen nun zur Abrundung dieses CNC-Kursabschnitts die jeweiligen Umkehrfunktionen von sin, cos und tan. Die Formeln dazu finden sich in den Abbildungen 8 bis 10. Auch hier gilt: Je genauer der zu errechnende Wert bestimmt werden soll, desto größer muss die Rechentiefe sein, was durch eine Verlängerung der jeweiligen Formel erreicht wird.
SIM_WORK ist ein reines Schulungssystem und daher nur mit begrenzten Fähigkeiten ausgestattet. Daher ist es leider nicht möglich, alle Makros komplett in den Speicher zu laden, da der Makrospeicher, ebenso wie der Hauptprogrammspeicher, maximal 99 Zeilen aufnehmen kann. Daher wird in diesen vorgestellten Beispielen lediglich per Programmlauf die Berechnung von Winkeln durchgeführt, ohne ein praktisches Werkstück zu programmieren. Dieser Schritt sollte auf einer realen Steuerung erfolgen, wenn man einen ausführlichen Probelauf auf dieser Steuerung vorgenommen hat. Probeläufe sind eine wichtige Vorsichtsmaßnahme, um teure Maschinenschäden zu vermeiden, sollte das CNC-Programm sich anders verhalten, als erwartet.
Zum Testen der Makros wird im Hauptprogramm zunächst ein Zahlenwert in den Parameterspeicher geschrieben und danach das gewünschten Makro aufgerufen, um den Rechenvorgang auszuführen. Soll beispielsweise der Sinus eines Winkels berechnet werden, wird zunächst der Parameter E70 mit dem Winkelwert in Grad geladen. Innerhalb der Makros erfolgt die Umwandlung in Bogenmaß, sowie die Ausgabe des Ergebnisses, das in den Parameterspeicher E99 geschrieben wird. Da CNC-Steuerungen keine direkte Ausgabe von Ergebnissen am Bildschirm kennen, muss das Ergebnis durch Anwahl von E99 manuell ausgelesen werden. Die Berechnung von Cosinus oder Tanges erfolgt auf identische Weise. Es muss lediglich der korrekte Aufruf des jeweiligen Makros beachtet werden, um Fehlberechnungen zu vermeiden.
Soll nun der errechnete Wert wieder in den Ausgangswinkel zurückgerechnet werden, so sind die Arcus-Funktionen einzusetzen. In diesem Fall wird der ermittelte Wert in den Parameter E70 geschrieben und das jeweilige Makro aufgerufen. Im Parameter E99 befindet sich danach der Winkel, der Bereits vom Bogenmaß in Grad umgerechnet wurde.

Abb.8 Arcussinus
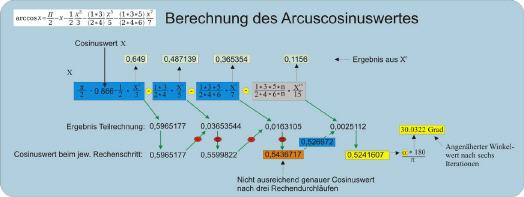
Abb9. Arcuscosinus
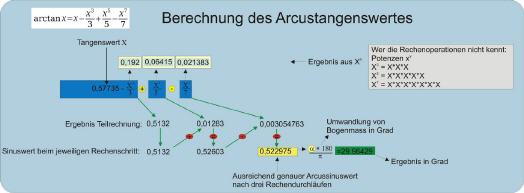
Abb10. Arcustangens
Arcussinusfunktion als CNC-Programm
%MM
N616161 (Arcussinus)
N10 (E70=Sinus des Winkels)
N12 (E40=Potenzwert)
N13 (E41=Ergebnis Potenzberechnung 3)
N14 (E42=Ergebnis Potenzberechnung 5)
N15 (E43=Ergebnis Potenzberechnung 7)
N17 (E60 bis E66=Berechnungszwischenspeicher)
N50 (E88=Angenaeherter Arcussinuswert nach Rechenschritt n)
N60 (E99=Ergebnis des Arcussinuswertes)
N70 (*** Potenz berechnen ***)
N71 E40=3
N71 E40=E40-2 (Schleifendurchlauf reduzieren)
N72 E41=E70 (Nennwert in Rechenvariable uebergeben)
N73 E41=E41*E70 (Potenzberechnung)
N74 G14 N1=73 N2=73 J=E40 (Schleife)
N75 E40=5
N76 E40=E40-2 (Schleifendurchlauf reduzieren)
N77 E42=E70 (Nennwert in Rechenvariable uebergeben)
N78 E42=E42*E70 (Potenzberechnung)
N79 G14 N1=78 N2=78 J=E40 (Schleife)
N80 E40=7
N81 E40=E40-2 (Schleifendurchlauf reduzieren)
N82 E43=E70 (Nennwert in Rechenvariable uebergeben)
N83 E43=E43*E70 (Potenzberechnung)
N84 G14 N1=83 N2=83 J=E40 (Schleife)
N85 (*** Ende Potenz berechnen ***)
N90 (*** Erster Rechenschritt ***)
N100 E60=E41/3
N102 E61=E60*0.5
N104 E88=E70+E61 (Ergebnis 1)
N150 (*** Zweiter Rechenschritt ***)
N190 E60=3/8
N192 E61=E42/5
N194 E62=E60*E61
N220 E88=E88+E62 (Ergebnis 2)
N235 (*** Dritter Rechenschritt ***)
N270 E63=15/48
N272 E64=E43/7
N274 E65=E63*E64
N280 E88=E88+E65 (Ergebnis 3)
N290 (*** Ergebnis in Grad umwandeln ***)
N300 E70=E88
N310 E70=E70*180
N320 E70=E70/3.141592654
N330 E99=E70 (Ergebnis in Grad)
Download
Den letzten Teil des CNC-Kurses können Sie hier als PDF-Datei herunterladen [2.010 KB]
. In dieser Datei findet sich zusätzlich ein Anhang mit einer Übersicht über den in SIM_WORK beziehungsweise der Philips 432-Steuerung vorhandenen CNC-Befehlssatz.
Die zum CNC-Kurs gehörenden CNC-Programme können Sie hier im selbstentpackenden 7ZIP-Format [130 KB]
herunterladen.
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 3 - gesamt: 15976.















































































