Zahnradmessung leicht gemacht
Den Zahnrädern auf den Zahn gefühlt
Mit Zahnrädern sind sehr präzise Übersetzungen möglich, was Zahnradgetriebe positiv von Riementrieben abhebt. Nur mit Zahnrädern sind daher akzeptabel genau laufende Uhren sowie präzise positionierbare Werkzeugmaschinen und Messgeräte realisierbar. Damit Zahnräder sich jedoch ohne übermäßiges Spiel beziehungsweise zu strengem Lauf abwälzen, müssen deren Werte akkurat berechnet und überprüft werden.

Während Riementriebe unkritisch herzustellen sind, muss beim Anfertigen von Zahnradgetrieben akribisch auf das Einhalten wichtiger Maße sowie auf die präzise Ausführung der einzelnen Zähne geachtet werden. Nur dann ist garantiert, dass sich Zahnräder sauber abwälzen und Drehmomente ohne übermäßigen Verschleiß der Zähne beziehungsweise unter großem Reibungsverlust übertragen werden können.
Aus diesem Grund ist es wichtig, sich mit den Formeln, Werkzeugen und Messmitteln rund um die Produktion von Zahnrädern auseinanderzusetzen. Es gilt, Zahnräder mit denjenigen Merkmalen anzufertigen, der es ihnen nach Fertigstellung erlaubt, den jeweils vorgesehenen Zweck zu erfüllen. Der Fachmann muss dazu verschiedenste Teilapparatmodelle beherrschen, den Begriff ›Modul‹ kennen und Messmittel sicher anwenden.
Während einzelne Zahnräder in der Regel mittels eines manuell bedienten Teilapparats hergestellt werden, greift man für die Serienfertigung auf CNC-Rundtische oder CNC-Teilapparate zurück. Moderne Technik bietet den Vorteil, dass die gewünschte Teilung des Zahnrads direkt in die CNC-Steuerung eingegeben werden kann, für das manuelle Teilen via Teilapparat jedoch das Bruchrechnen anzuwenden ist, damit das benötigte Zahnrad einwandfrei produziert werden kann.
Der Weg zum Zahnrad
Die Kenntnis von Begriffen, wie etwa ›Kopfspiel‹, ›Achsabstand‹ oder ›Zahnfußhöhe‹ ist eine wichtige Voraussetzung, damit Zahnräder korrekt hergestellt werden. Ganz wichtig in diesem Kontext ist der Begriff ›Modul‹.
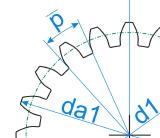
Der Modul ist nichts anderes, als ein Maß für die Größe der Zähne eines Zahnrades und wird in Millimeter angegeben. Er besitzt das Kürzel ›m‹ und ist das Ergebnis einer Division der Zahnradteilung p durch die Kreiszahl Pi.
Wem der Begriff ›Zahnradteilung‹ nichts sagt: Dies ist der Abstand zweier benachbarter Zahnradzähne. Der Modul ist Dreh- und Angelpunkt bei der Zahnradberechnung. Ohne vorab diesen Wert berechnet zu haben, sind keine weiteren Schritte zur Zahnradberechnung möglich.
Die Teilung p, also der Abstand zwischen zwei Zähnen, ist das Ergebnis einer Multiplikation des Moduls mit der Kreiszahl Pi. Die Zahl aus dieser Berechnung ist das Bogenmaß eines Abschnitts von Zahn zu Zahnlücke. Noch einfacher ausgedrückt: Die berechnete Zahl ist ein Teil des Umfangs vom Teilkreisdurchmesser d.
Dies lässt sich anhand einer Musterrechnung rasch nachprüfen:
Teilkreisdurchmesser d=150mm
Teilkreisumfang=150*Pi=471,2388mm
Modul m=5
Zähnezahl z=30
Teilung p=m*pi=15,707963
Teilkreisumfang=p*z=471,2388mm
Aus dieser Musterrechnung kann man ersehen, dass das Bogen- und das Winkelmaß zusammenhängen. In beiden Fällen wird mit einer Zahl der Anteil eines Abschnitts zum Ganzen ausgedrückt.
Der Winkel zwischen dem Bereich Zahn-Zahnlücke (man könnte auch sagen „zwischen Zahnmitte und Zahnmitte“) beträgt 360/30=12 Grad, während das Bogenmaß für exakt diesen Winkel bezogen auf den Teilkreis von 150 Millimeter Durchmesser 15,707963 Millimeter beträgt.
Vorgehen beim Zahnradrechnen:
In der Regel stellt sich die Aufgabe, mit Zahnrädern ein bestimmtes, konstantes Übersetzungsverhältnis zu erreichen. Insbesondere bei Uhren und Messmitteln werden genau gefertigte Zahnräder eingesetzt, um die Zeit oder Maßabweichungen exakt messen zu können. Die Übersetzungen müssen daher höchst präzise berechnet werden, damit entsprechend gefertigte Zahnradgetriebe ihre Aufgabe optimal erfüllen können.
Bei Zahnrädern ist der alles entscheidende Wert einer exakten Übersetzung die Größe der beiden Teilkreisdurchmesser, die sich beim Ineinandergreifen der Zähne präzise berühren müssen. Erst wenn diese Durchmesser bekannt sind, kann das dazu passende Zahnrad berechnet werden.
Beispiel:
Es ist eine Zahnradkombination gewünscht, die es erlaubt, eine Drehzahl von 100 auf 66,67 Umdrehungen pro Minute zu senken. Das Übersetzungsverhältnis beträgt also 1,5:1. Besitzt das treibende Rad einen Teilkreisdurchmesser von 100 Millimeter, so muss das getriebene Rad einen Teilkreisdurchmesser von 100*1,5=150 Millimeter besitzen.
Die Wahl des passenden Moduls ist eine wesentliche Überlegung bei der Herstellung von Zahnrädern. Dazu ist zu ermitteln, welcher Belastung die Zähne ausgesetzt sind, also welches Drehmoment auf diese einwirkt. Entsprechend muss der Modulwert gewählt werden, damit die Zähne groß genug sind, um die Last aufzunehmen. Doch gilt es auch zu berücksichtigen, dass zu große Zähne das Laufgeräusch und den Kraftbedarf durch den höheren Widerstand beim Abwälzen der Zähne erhöhen. Es ist also die Erfahrung des Konstrukteurs gefragt, den passenden Modulwert auszuwählen.

Modul 16
Ein Modul von 16 Millimeter ist für große Zähne optimal, in diesem Fall jedoch wohl zu groß. Z1=9; Z2=9 Ein Modul von 16 Millimeter ist für große Zähne optimal. Diese können viel Kraft aufnehmen, laufen jedoch geräuschvoll.

Modul 1
Ein Modul von 1 Millimeter ist für den vorgesehenen Zweck möglicherweise zu klein. Z1=100; Z2=150 Ein Modul von 1 Millimeter erzeugt kleine Zähne. Diese laufen leise, können jedoch nur wenig Kraft aufnehmen.
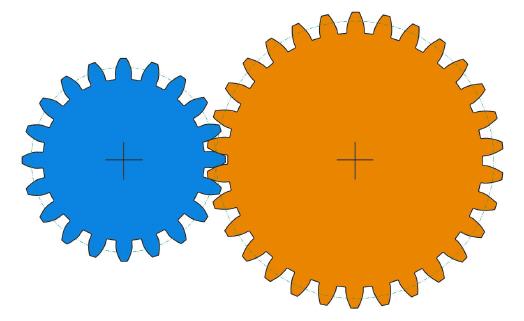
Modul 5
Ein Modul mit 5 Millimeter ist für den vorgesehenen Zweck optimal. Die Zähne sind nicht zu groß und nicht zu klein. Z1=20; Z2=30. Die Wahl des passenden Moduls ist Sache des Konstrukteurs, der auch die entscheidenden Zahnradmaße berechnet.
Nachdem nun der passende Modulfräser ausgewählt wurde, kann die Zahnradfertigung starten. Während der Fertigung müssen immer wieder die Maße des entstehenden Zahnrads kontrolliert werden, um festzustellen, ob das Sollmaß bereits erreicht ist. Dabei ist zu beachten, dass Zahnräder in einer bestimmten Toleranz hergestellt werden müssen, damit es im Verbund mit anderen Zahnrädern ein sauberes Ineinandergreifen der jeweiligen Zähne gibt.
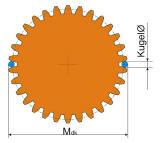
Messmittelproduzenten, wie etwa das Unternehmen Mitutoyo haben für diesen Zweck manuell bedienbare Messgeräte im Portfolio: Für kleinere Zahnräder ein Zahnradmikrometer mit Kugeleinsätzen und für größere Zahnräder eine Bügelmessschraube mit Tellermessfläche.
Wichtig ist zu wissen, dass der Praktiker an der Maschine keinerlei Berechnungen anstellen muss, die das von ihm gefertigte Zahnrad betreffen. Alle Angaben findet er in der zum Zahnrad gehörenden technischen Zeichnung. Seine Fertigkeit begrenzt sich auf das korrekte Kalibrieren der Messmittel, damit die vorgegebenen Zahnradmaße exakt gemessen werden können.
Der Kalibriervorgang ist insbesondere beim Messen mit der Bügelmessschraube wichtig, da dieses Messgerät über auswechselbare Kugeleinsätze verfügt und nach jedem Wechsel dieser Einsätze der Nullpunkt des Messgeräts verloren geht. Beim Einstellvorgang ist zu beachten, dass die Durchmessersumme der beiden Kugeln berücksichtigt wird. Bei einem verwendeten Kugeldurchmesser von fünf Millimeter und Nutzung einer Bügelmessschraube mit dem Messbereich 0 bis 25 Millimeter ist die Referenz beim Wert zehn, während eine Bügelmessschraube mit dem Messbereich 50 bis 75 Millimeter den Wert 60 als Referenz bekommt.
Von klein bis groß
Die zu verwendende Kugelgröße der Einsätze richtet sich nach der Zahngröße des zu messenden Zahnrades. Je kleiner die Zähne sind, desto kleiner muss auch die zum Messen verwendete Kugel sein. Der kleinste von Mitutoyo angebotene Einsatz besitzt eine Kugel mit einem Durchmesser von 0,8 Millimeter, der größte Einsatz misst hingegen acht Millimeter. Wer alle Einsätze besitzt, kann Zahnräder mit einem Modul von circa 0,5 bis circa 4,0 messen. Zahnräder mit einem Modul kleiner 0,5 Millimeter sind so klein, dass sie nur mehr mit einem Koordinatenmessgerät gemessen werden können.

Nachfolgend eine Tabelle der zum Zahnradmessen üblichen Kugeldurchmesser:
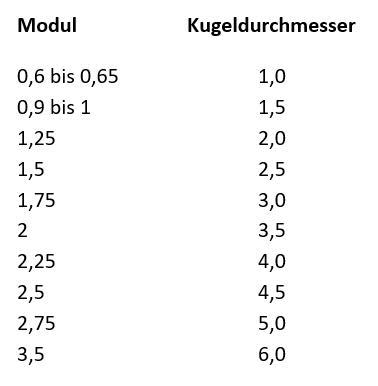
Für größere Zahnräder bietet sich das Messen der Zähne mit dem Tellermikrometer an. Auch in diesem Fall muss der Praktiker keine Berechnungen durchführen, sondern kann alle nötigen Maße der technischen Zeichnung entnehmen. Hier findet er die Zahl der Zähne, die zwischen den Tellerflächen eingenommen werden müssen und das obere sowie untere Abmaß, zwischen dem das Istmaß liegen muss.
Die Wahl zwischen den beiden Messverfahren hängt insbesondere vom Modul, aber auch von den Vorlieben des Fachmanns ab.

Der Weg zum Zweikugelmaß
Heute muss niemand mehr die Prüfmaße mühsam von Hand ermitteln. Dazu stehen leistungsstarke Programme beziehungsweise Excel-Tabellen zur Verfügung. Nichtsdestotrotz ist es natürlich interessant zu erfahren, wie die von diesen Programmen getätigten Rechenschritte aussehen.
Die Evolvente:
Zahnräder mit Evolventenprofil sind heute diejenigen, die am häufigsten angetroffen werden. Diese Zahnform wird insbesondere im Maschinenbau bevorzugt. Wenn Zahnräder mit Evolventenprofil hergestellt werden sollen, stellt sich zunächst die Frage, wie eine Evolvente überhaupt erzeugt wird.
Diese Frage kann man sehr anschaulich mithilfe eines Fadens und eines Kochtopfdeckels gleich selbst beantworten: Ein Evolventenprofil entsteht automatisch, wenn ein um den Deckel gewickelter Faden durch ziehen am Fadenende stramm gespannt wird und vom Deckel im Uhrzeiger oder Gegenuhrzeigersinn abgewickelt wird. Ein mitlaufender Bleistift würde das Evolventenprofil auf ein Stück Papier kenntlich machen.
Die Evolventenform kann jedoch auch mittels eines CAD-Systems ermittelt werden. Dazu genügt es, einen beliebig großen Kreis zu zeichnen und an diesem eine Tangente entlanglaufen zu lassen. Zu beachten ist allerdings, dass die Länge der Tangente für unterschiedliche Winkellagen berechnet werden muss, damit sich der Fadeneffekt einstellt.
Der Grundkreis:
Der Ausgangspunkt jeder Zahnradkonstruktion ist zunächst einmal die Wahl eines Moduls sowie die Festlegung einer Zähnezahl. Stehen diese Parameter fest, so können daraus der Teilkreis- sowie der Grundkreisdurchmesser berechnet werden. Der Grundkreisdurchmesser spielt die Rolle des „Kochtopfdeckels“, an dem sich der stramm gespannte „Faden“ entlangbewegt. Wird versehentlich der Teilkreisdurchmesser als Anlage für die Tangente verwendet, so wird das Profil falsch konstruiert.
Angenommen, es wird ein Modul 5 und eine Zähnezahl 10 verwendet, so lautet die Formel zum Berechnen des Teilkreisdurchmessers wie folgt:
d=z x m
d= 10 x 5
d=50 mm
Auf der Grundlage dieses Ergebnisses kann nun der Grundkreis berechnet werden:
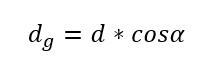
Diese Formel kann noch nicht gelöst werden, da der zu verwendende Winkel noch unbekannt ist beziehungsweise noch nicht erläutert wurde, welcher Winkel hier eingesetzt werden kann. Dazu ist anzumerken, dass im Mittenbereich des Verzahnungsprofils erfahrungsgemäß ein Winkel von etwa 20 Grad vorliegt, der daher genormt wurde und als Eingriffswinkel Alpha bezeichnet wird. Wird dieser Winkel in die Formel eingesetzt, so lautet das Ergebnis für den Grundkreis dg:
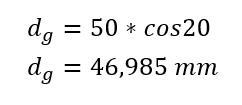
Am Grundkreis wird nun der „Faden“ abgewickelt, um das Evolventenprofil für die Zahnradzähne zu erzeugen. Diese Rolle übernehmen Tangenten, die entlang des Grundkreises in einem vorher festgelegten Winkel positioniert werden. Doch dies ist nur die halbe Miete. Vorab muss auch noch berechnet werden wie lang diese Tangenten werden müssen, damit die entlang der Enden der Tangenten sich entlangbewegenden Geraden das Evolventenprofil ergeben.
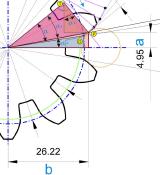
Wie das Gedankenmodell des Fadens zeigt, sind die Längen der Tangenten nichts anderes als der jeweils gestreckte Bogenabschnitt eines bestimmten Winkels Alpha, der die Punkte O und T einschließt. Dieser Bogenabschnitt ergibt im ausgestreckten Zustand die Strecke T-P. Wird dieser Vorgang mit verschiedenen Teilungswinkel wiederholt, ergeben die aneinandergereihten Punkte P schlussendlich die Evolventenkontur eines Zahnradzahns.
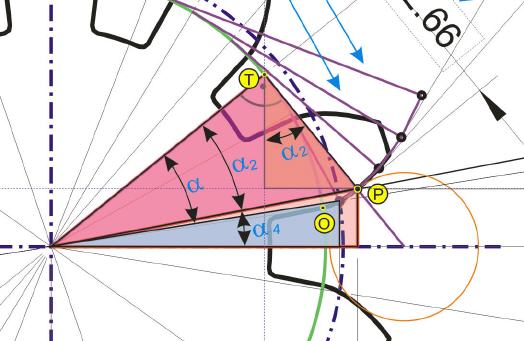
Während eine einfache Umfangsberechnung die Länge des Bogens zwischen dem jeweilig eingeschlossenen Winkel ergibt, kann mit den Winkelfunktionen die dazu passende Lage des Endpunkts der Strecke berechnet werden.
Die Bogenlänge eines bestimmten Winkels ergibt sich aus folgender Formel:
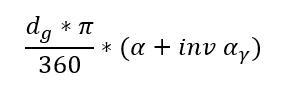
Da der Eingriffswinkel in der Regel 20 Grad beträgt, ergibt sich für die inv-Funktion der Winkelwert 0,854 Grad, der zum Teilungswinkel dazugerechnet werden muss. Dieser Winkel ergibt sich wie folgt aus der Involutfunktion:
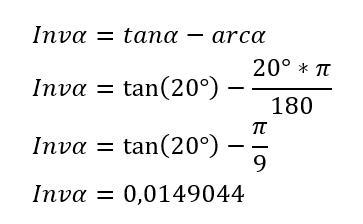
Das Ergebnis liegt nun im Bogenmaß vor und muss anschließend noch in Grad umgerechnet werden. Die Formel dazu lautet:
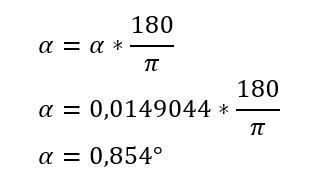
Da der Grundkreisdurchmesser dg 46,985 mm beträgt, ergeben sich für die vorab festgelegten Teilungswinkel folgende Bogenlängen:
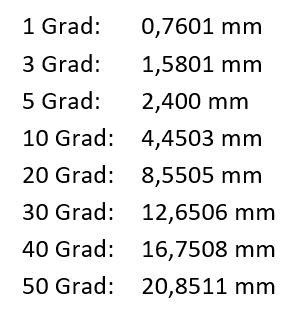
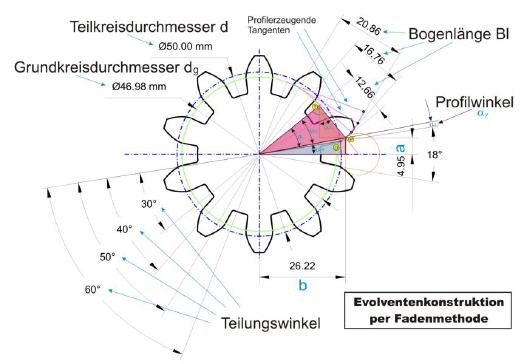
Um die Berechnung dieser Tabelle zu verdeutlichen, nachfolgend das Beispiel für 30 Grad:
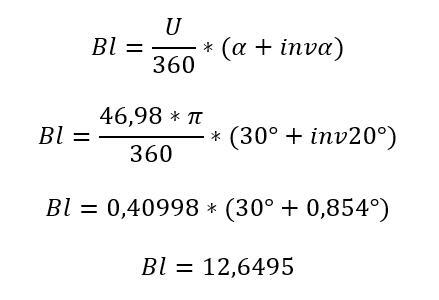
Die leichte Abweichung zum Ergebnis in der Tabelle ist Rundungsfehlern geschuldet.
Die Länge der Bogenlänge Bl entspricht der Länge der jeweiligen Strecke T-P, die wiederum der Ankathete in einem rechtwinkligen Dreieck entspricht. Nachdem diese Werte bekannt sind, können die Koordinaten errechnet werden, durch die sich die Kurve beziehungsweise die Evolvente der Zahnradkontur ergibt.
Folgend eine Tabelle mit Endpunkt-Koordinaten:
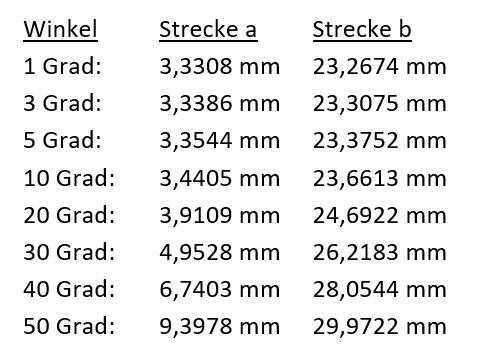
Um die Berechnung dieser Tabelle zu verdeutlichen, nachfolgend ein Beispiel für einen Teilungswinkel von 30 Grad. Dazu ist es zunächst nötig, die fehlenden Winkel zu ermitteln:

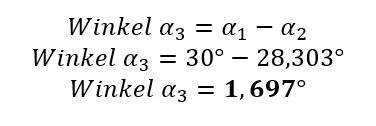
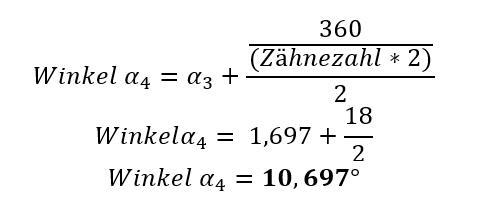
Nun können die Elemente des rechtwinkligen Dreiecks ermittelt werden:

Auf diese Weise könnten auch alle Punkte zur Prüfung eines Zahnrades auf Messmaschinen berechnet werden. Doch dies ist nicht im Fokus dieses Artikels. Hier geht es darum, das Zweikugelmaß zu ermitteln, um ein fertiggestelltes Zahnrad auf das Einhalten der Maße überprüfen zu können.
Dazu ist es ganz wichtig zu wissen, dass zur Berechnung des Zweikugelmaßes kein Winkel verwendet wird, dessen daraus resultierenden Konstruktionspunkte für die Zahnradevolvente unterhalb des Teilkreises liegen, da nur ein Berührpunkt oberhalb des Teilkreises eine sichere Anlage der Kugel beziehungsweise eines Drahtes ermöglicht.
Sicher geht, wer folgende Formel zur Prüfung verwendet:
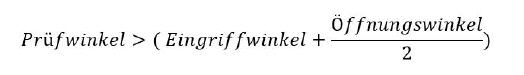
Beträgt beispielsweise der Eingriffswinkel 20 Grad und der Öffnungswinkel 18 Grad, so ergibt sich ein Prüfwinkel von 29 Grad, der auf jeden Fall als Mindestwinkel anzusehen ist. Auf der sicheren Seite steht, wer mindestens ein Grad, besser noch mehr Grad aufschlägt.
Der Weg zum Prüfmaß:
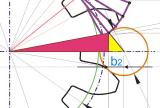
Um nun das Prüfmaß zur Feststellung der korrekten Fertigung des Zahnrades zu ermitteln, muss zunächst der Berührpunkt zweier Zahnflanken mit einem Prüfkörper ermittelt werden. Diese beiden Berührpunkte liegen exakt gegenüber und werden von einem Kreis durchdrungen. Dieser Kreis kann Bestandteil eines Zylinders oder einer Kugel sein. Es spielt also keine Rolle, welche Körperform bei der Zahnradprüfung zum Einsatz kommt.
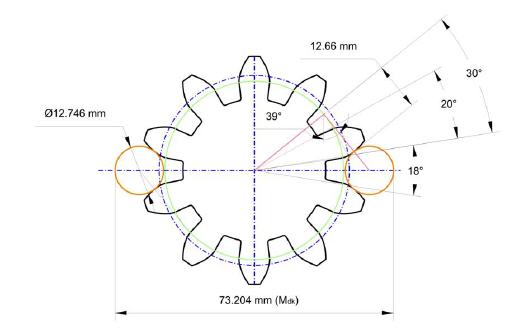
Wenn davon ausgegangen wird, dass ein Teilungswinkel von 30 Grad der nachfolgenden Berechnung zugrunde liegt, so ergibt sich der Durchmesser des Prüfkreises aus folgender Formel:

Ist der Kugeldurchmesser bekannt, muss noch die Strecke b2 berechnet werden, damit schlussendlich die Ermittlung des Zweikugelmaßes Mdk möglich wird.
Die Formel lautet:
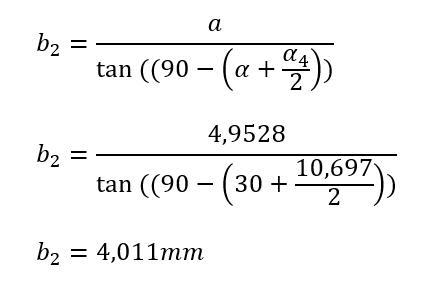
Gesetzt den Fall, es gäbe eine Kugel oder einen Zylinder mit dem Durchmesser von 12,746 Millimeter, dann würde sich das Zweikugelmaß Mdk wie folgt ergeben:
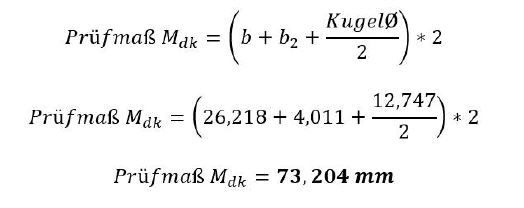
Durch das Anfertigen eines Zylinders mit dem Durchmesser 12,747 mm könnte man nun mit der Prüfung der produzierten Zahnräder beginnen. Eleganter ist es jedoch, auf die im Handel zu bekommenden Kugeln und Zylinder zurückzugreifen, die diese Arbeit ersparen. Diese besitzen jedoch eine gerade Zahl im Durchmesser, weshalb das Maß Mdk neu berechnet werden muss.
Soll beispielsweise eine Kugel oder ein Zylinder mit dem Durchmesser von 12 Millimeter verwendet werden, so liegt der gesuchte Winkel, der zu diesem Prüfmaß passt, zwischen 28 und 29 Grad. Die Ermittlung des Wertes ist leider nur iterativ möglich, sodass ein Excel-VBA-Programm eingesetzt werden müsste, um die Lösung zu ermitteln. Möglich ist aber auch der Einsatz des Solvers von Excel, der sich für diesen Zweck anbietet.
Der Solver
Bevor der Solver in Excel genutzt werden kann, muss dieser zunächst aktiviert werden, da dies ein Add-In ist, das nicht mit der Installation von Excel automatisch eingebunden wird.
Der Solver ist nichts anderes, als eine Eingabemaske für eine Iterationsschleife, in der ein gesuchter Wert durch automatisches Verändern von Variablen ermittelt wird. Allerdings muss diese Maske mit wohlüberlegten Werten gefüttert werden, damit das gewünschte Ergebnis berechnet wird. Da Rundungsfehler signifikant ins Gewicht fallen können, ist anzuraten, die errechneten Werte kritisch zu betrachten und eventuell einen Korrekturfaktor zu nutzen, der zu große Abweichungen von korrekten Maßen verhindert.
Nachdem der Solver aktiviert wurde, findet sich sein Start-Button im Menü ›Daten‹. Ein Mausklick auf diesen Button lässt eine Eingabemaske erscheinen, in die diverse Werte einzugeben sind.
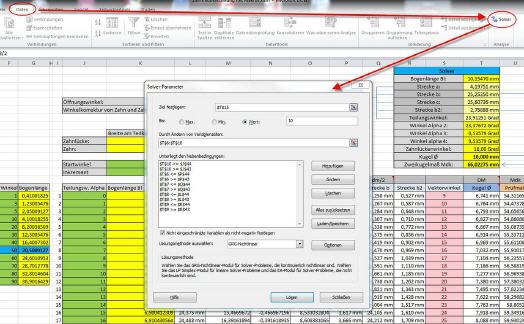
Eingabe des Ziel-Kugeldurchmessers:
Wie bereits erwähnt, ist es zur Ermittlung des Mdk-Werts nötig, für den Solver-Rechenlauf einen Ziel-Kugeldurchmesser zu verwenden, den frei beschaffbare Kugeln üblicherweise besitzen. Darüber hinaus ist zu berücksichtigen, dass die Kugeln sich möglichst nahe am Teilkreis an die Evolvente der Zähne anschmiegen sollen, jedoch immer oberhalb dieses Maßes am Zahn anliegen müssen.
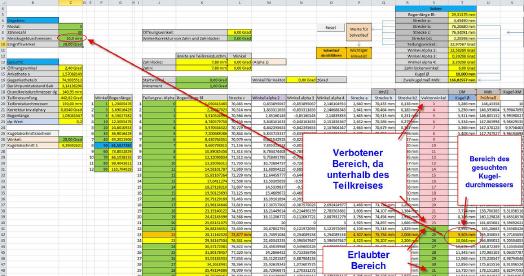
Solver-Rechenlauf vorbereiten:
Da der Solver bei jedem erfolgreichen Rechenlauf die Formeln in den verwendeten Zellen löscht und dort die Ergebnisse einträgt, muss die Excel-Tabelle so aufgebaut werden, dass vor einem erneuten Solverlauf die dazu nötigen Formeln wieder in die entsprechenden Zellen geschrieben werden.
Die Variablen, die bereits in der Tabelle stehen, ergeben einen ganz bestimmten Kugeldurchmesser. Im konkreten Beispiel werden als kleinster Durchmesser das Maß 9,505 mm und als größter Durchmesser das Maß 10,064 mm berechnet. Irgendwo dazwischen verbergen sich die konkreten Maße, mittels derer sich der gewünschte Kugeldurchmesser von 10 Millimeter ergeben würde. Der Solver verändert in mehreren Durchläufen so lange die Werte dieser Variablen, bis sich der gesuchte Wert aus den immer wieder neu ermittelten Werten ergibt.
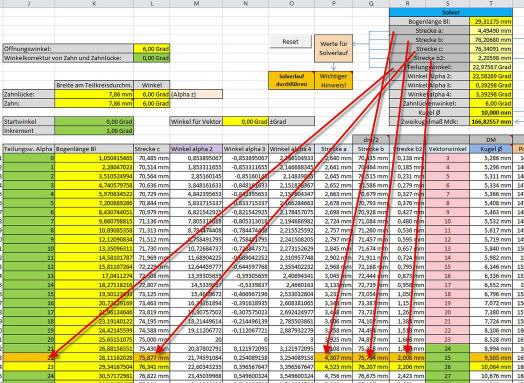
Ganz wichtig ist vor dem Solverlauf die Festlegung von Nebenbedingungen, damit keine falschen Werte ermittelt werden. Diese würden unter Umständen nicht einmal auffallen, da sie ebenfalls zum gewünschten Kugeldurchmesser führen, jedoch einen völlig falschen Mdk-Wert zur Folge hätten.
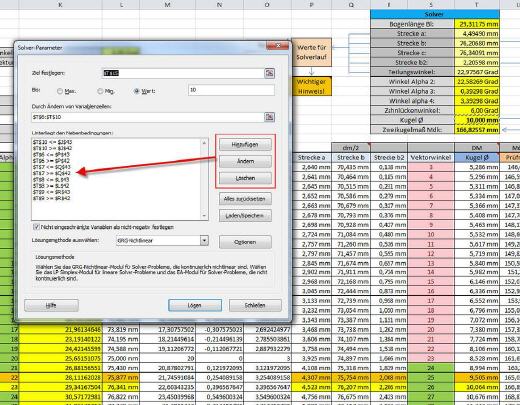
Grundsätzlich geht es zur Berechnung des korrekten Mdk-Werts bei den Nebenbedingungen darum, dem Solver zusagen, in welchen Grenzen er die Variablen verändern darf, um zum gewünschten Ergebnis zu kommen. Doch ist es nicht damit getan, den Solver entlang des Wertebandes von 9,505 und 10,064 Millimeter suchen zu lassen, da der Wert des gesuchten Durchmessers von zehn Millimeter näher an 10,064 Millimeter liegt, als am Wert 9,505 Millimeter. Der Unterschied beträgt 0,064 zu 0,495 Millimeter.
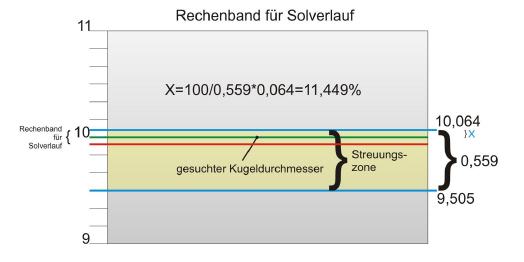
Insbesondere wenn mehrere Variablen veränderbar sind, muss bei der Nutzung des Solvers zudem darauf geachtet werden, dass diese in Zielrichtung größer werdender Werte gewählt werden, da sonst das Ergebnis nicht korrekt ist.
Im Beispiel der Kugelberechnung muss daher als Startwert für den Teilungswinkel aus der groben Excel-Tabelle derjenige Wert gewählt werden, der unterhalb des Zielwerts liegt. Da der Kugeldurchmesser beim Teilungswinkel von 29 Grad 25,227 Millimeter beträgt und bei 28 Grad 11,744 Millimeter ausgewiesen werden, ist der Teilungswinkel von 28 Grad für die Berechnung der Werte für einen Kugeldurchmesser von 12 Millimeter zu verwenden. Infolgedessen beträgt der dazugehörende Wert für die Strecke a 4,689651514 Millimeter.
Der Berechnung des realen Kugeldurchmessers liegt folgende Formel zugrunde:
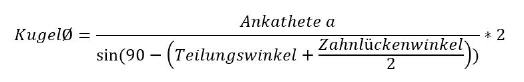
Diese Formel verwendet der Solver zum Berechnen der Parameter ›Ankathete a‹ und ›Teilungswinkel‹ aus denen sich der Kugeldurchmesser von 12 Millimeter ergibt. Der Zahnlückenwinkel bleibt außen vor, da dieser aktuell unverändert bleibt. Dieser würde erst dann ins Spiel kommen, wenn das Zahnrad mit einem leichten Spiel gefertigt werden soll. In diesem Fall müsste dieser Wert als dritter Parameter in der Solver-Eingabemaske berücksichtigt werden.
Nach dem Solverlauf wird das Ergebnis wie folgt präsentiert:
Ankathete a = 4,77936 Millimeter
Teilungswinkel = 28,19724 Grad
Werden diese Werte in die Formel eingesetzt, so ergibt sich ein Kugeldurchmesser von genau 12 Millimeter, wie eine Überprüfung mit dem Taschenrechner bestätigt:

Übrigens: Es ist nicht nötig, die Werte von Hand in die Tabelle für den Solver einzutragen. Die Werte können gefahrlos auch per Zellverweis übernommen werden, da der Solver die Quellzellen nicht ändert.
Bleibt nur noch die Ermittlung des Zweikugelmaßes Mdk. Dieses Maß ergibt sich aus folgender Formel:
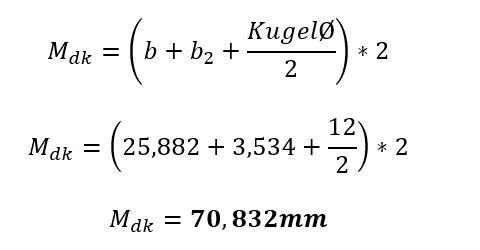
Messen größerer Zahnräder
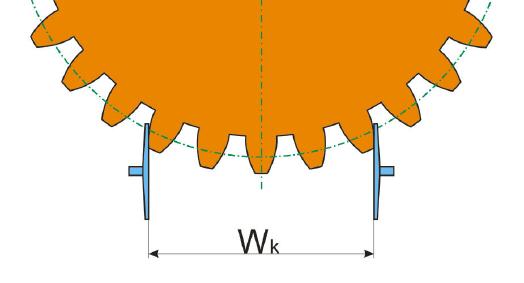
Die eben erwähnte Zweikugelmaßmethode wird für kleinere Zahnräder genutzt. Größere Zahnräder misst man mit einem Tellermikrometer. Dazu muss die Zahnweite Wk ermittelt werden. Um diese zu ermitteln, muss zunächst berechnet werden, wie viele Zähne sinnvollerweise in die Messung einzubeziehen sind. Es sollen folgende Werte angenommen werden:
Modul m: 2 mm
Zähnezahl z: 36
Öffnungswinkel Alpha: 20 Grad
Profilverschiebungsfaktor: 0,3
Berechnung von Involut Alpha: Die Formel zum Berechnen der Involutfunktion wurde weiter oben bereits durchgenommen, weshalb hier auf eine Wiederholung verzichtet wird. Das Ergebnis bei einem Öffnungswinkel von 20 Grad lautet: 0,0149 Grad.
Zähnezahl für die Messung k: Zum Ermitteln der für das Messen des Maßes Wk nötigen Zähnezahl ist folgende Formel heranzuziehen:
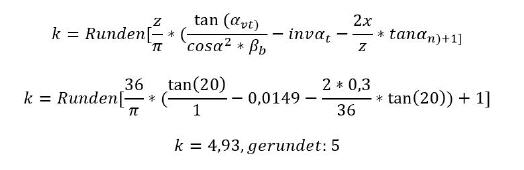
Anmerkung: In der Formel steht der Begriff „Runden“ für die Rechenfunktion „INT“. Es wird die Zahl also als ganzzahliger Wert ohne Nachkommastellen ausgegebene.
Ermitteln des Maßes Wk:
Zur Ermittlung des Maßes Wk ist folgende Formel nötig:
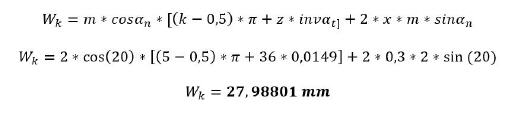
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 7 - gesamt: 37307.